Динамическое программирование — популярный метод в компьютерных науках и разработке программного обеспечения, который играет решающую роль в спортивном программировании. Это метод решения сложных проблем путем их разбиения на более мелкие подзадачи и решения каждой подзадачи только один раз с сохранением решений подзадач, чтобы их можно было повторно использовать при необходимости. В этой статье мы рассмотрим необходимые алгоритмы динамического программирования, которые должен знать каждый, кто увлекается спортивным программированием.
1. Числа Фибоначчи
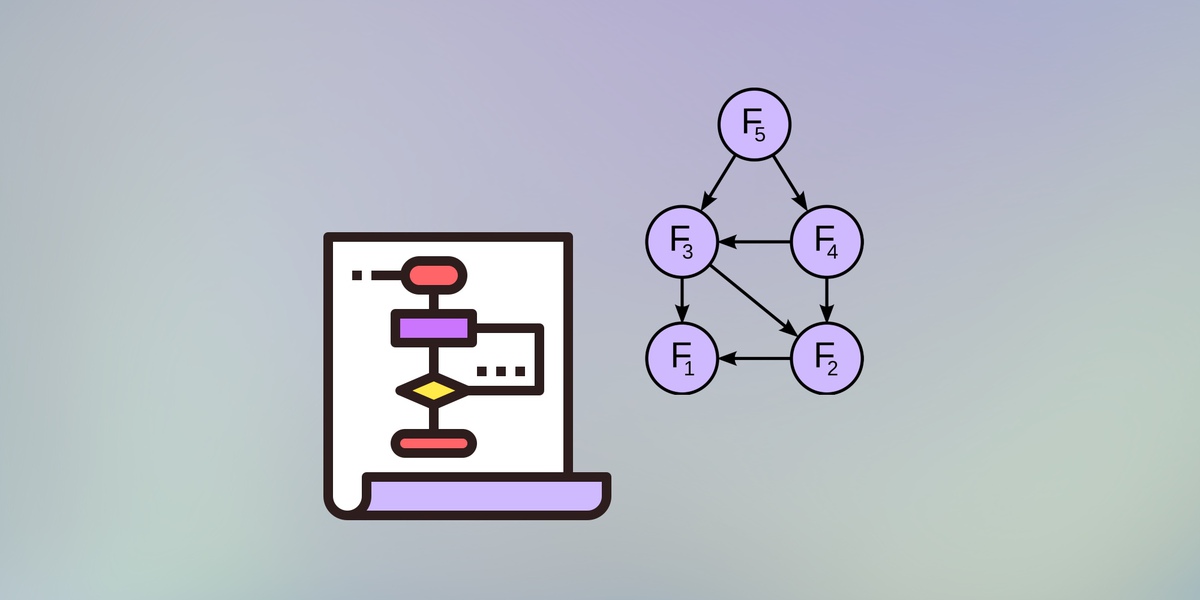
Последовательность Фибоначчи — это хорошо известная последовательность чисел, определяемая рекуррентным соотношением F(n) = F(n-1) + F(n-2), где F(0) = 0 и F(1) = 1. Простым рекурсивным алгоритмом вычисления чисел Фибоначчи было бы прямое использование рекуррентного соотношения, но это привело бы к экспоненциальной временной сложности. Динамическое программирование позволяет решить эту задачу за линейное время с помощью мемоизации, которая сохраняет результаты уже решенных подзадач.
def fibonacci(n, memo):
if n in memo:
return memo[n]
if n <= 1:
memo[n] = n
else:
memo[n] = fibonacci(n-1, memo) + fibonacci(n-2, memo)
return memo[n]
2. Самая длинная общая подпоследовательность
Задача о самой длинной общей подпоследовательности (LCS) — это классическая задача динамического программирования, которая включает в себя поиск самой длинной подпоследовательности, общей для двух заданных строк. Подпоследовательность строки — это последовательность символов, которые появляются в строке в одном и том же порядке, но не обязательно последовательно.
def lcs(s1, s2):
m, n = len(s1), len(s2)
dp = [[0] * (n+1) for _ in range(m+1)]
for i in range(1, m+1):
for j in range(1, n+1):
if s1[i-1] == s2[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[m][n]
3. Задача о рюкзаке
Задача о рюкзаке — это классическая задача оптимизации, которая включает в себя поиск оптимального подмножества предметов для упаковки в рюкзак с конечной вместимостью, чтобы максимизировать ценность упакованных предметов.
def knapsack(W, wt, val, n):
dp = [[0] * (W+1) for _ in range(n+1)]
for i in range(1, n+1):
for w in range(1, W+1):
if wt[i-1] <= w:
dp[i][w] = max(val[i-1] + dp[i-1][w-wt[i-1]], dp[i-1][w])
else:
dp[i][w] = dp[i-1][w]
return dp[n][W]
4. Расстояние Левенштейна (редакционное расстояние)
Задача редактирования расстояния заключается в нахождении минимального количества операций, необходимых для преобразования одной строки в другую. Допустимые операции: вставка, удаление и замена.
def edit_distance(s1, s2):
m, n = len(s1), len(s2)
dp = [[0] * (n+1) for _ in range(m+1)]
for i in range(m+1):
for j in range(n+1):
if i == 0:
dp[i][j] = j
elif j == 0:
dp[i][j] = i
elif s1[i-1] == s2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = 1 + min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1])
return dp[m][n]
5. Самый большой подмассив
Задача о самом большом подмассиве заключается в поиске непрерывного подмассива в одномерном массиве чисел с наибольшей суммой.
def max_subarray(arr):
n = len(arr)
max_sum = float('-inf')
current_sum = 0
for i in range(n):
current_sum += arr[i]
max_sum = max(max_sum, current_sum)
current_sum = max(current_sum, 0)
return max_sum
6. Размен монет
Проблема размена монет включает в себя поиск количества способов внести сдачу на заданную сумму денег, используя заданный набор номиналов монет.
def coin_change(coins, amount):
dp = [float('inf')] * (amount+1)
dp[0] = 0
for i in range(1, amount+1):
for coin in coins:
if coin <= i:
dp[i] = min(dp[i], dp[i-coin] + 1)
return dp[amount] if dp[amount] != float('inf') else -1
7. Умножение цепочки матриц
Задача умножения цепочек матриц заключается в поиске оптимального способа умножения ряда матриц. Это классический пример динамического программирования, который используется во многих областях, таких как компьютерная графика, численный анализ и научные вычисления.
def matrix_chain_order(p):
n = len(p) - 1
m = [[float('inf')] * n for _ in range(n)]
s = [[0] * n for _ in range(n)]
for i in range(n):
m[i][i] = 0
for l in range(2, n+1):
for i in range(n-l+1):
j = i + l - 1
for k in range(i, j):
q = m[i][k] + m[k+1][j] + p[i] * p[k+1] * p[j+1]
if q < m[i][j]:
m[i][j] = q
s[i][j] = k
return m, s
8. Самая длинная возрастающая подпоследовательность
Проблема самой длинной растущей подпоследовательности (LIS) включает в себя поиск самой длинной подпоследовательности заданной последовательности, которая строго возрастает. Проблема LIS имеет множество реальных приложений, таких как сжатие данных, распознавание образов и биоинформатика.
def lis(arr):
n = len(arr)
dp = [1] * n
for i in range(1, n):
for j in range(i):
if arr[i] > arr[j]:
dp[i] = max(dp[i], dp[j] + 1)
return max(dp)
9. Задача коммивояжера
Задача коммивояжера (TSP) заключается в поиске кратчайшего возможного маршрута, который проходит через заданный набор городов и возвращается в начальный город. TSP — это классическая задача информатики, которая имеет множество реальных приложений, таких как логистика, транспорт и оптимизация сети.
def tsp(graph, start):
n = len(graph)
visited = (1 << n) - 1
memo = {}
def dfs(node, visited):
if visited == 0:
return graph[node][start]
if (node, visited) in memo:
return memo[(node, visited)]
ans = float('inf')
for i in range(n):
if visited & (1 << i):
ans = min(ans, graph[node][i] + dfs(i, visited ^ (1 << i)))
memo[(node, visited)] = ans
return ans
return dfs(start, visited)
10. 0-1 Целочисленное программирование
Задача целочисленного программирования 0-1 включает в себя поиск оптимального решения для набора двоичных переменных решения с учетом набора ограничений. Задача целочисленного программирования 0-1 имеет множество практических применений, таких как распределение ресурсов, составление расписания и производственное планирование.
def knapsack(W, wt, val, n):
dp = [[0] * (W+1) for _ in range(n+1)]
for i in range(1, n+1):
for w in range(1, W+1):
if wt[i-1] <= w:
dp[i][w] = max(val[i-1] + dp[i-1][w-wt[i-1]], dp[i-1][w])
else:
dp[i][w] = dp[i-1][w]
return dp[n][W]
11. Расстояние Левенштейна с разрешенными операциями
Задача «Расстояние Левенштейна» может быть расширена, чтобы разрешить только определенный набор операций редактирования, таких как вставка, удаление и замена.
def edit_distance_with_allowed_ops(s1, s2, allowed_ops):
m, n = len(s1), len(s2)
dp = [[0] * (n+1) for _ in range(m+1)]
for i in range(m+1):
dp[i][0] = i
for j in range(n+1):
dp[0][j] = j
for i in range(1, m+1):
for j in range(1, n+1):
if s1[i-1] == s2[j-1]:
dp[i][j] = dp[i-1][j-1]
elif allowed_ops.get((s1[i-1], s2[j-1])):
op_cost = allowed_ops[(s1[i-1], s2[j-1])]
dp[i][j] = min(dp[i-1][j] + op_cost[0], dp[i][j-1] + op_cost[1], dp[i-1][j-1] + op_cost[2])
else:
dp[i][j] = 1 + min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1])
return dp[m][n]
12. Самая длинная палиндромная подстрока
Задача «Самая длинная палиндромная подстрока» заключается в поиске самой длинной подстроки заданной строки, которая является палиндромом.
def longest_palindromic_substring(s):
n = len(s)
dp = [[False] * n for _ in range(n)]
max_len = 1
start = 0
for i in range(n):
dp[i][i] = True
for l in range(2, n+1):
for i in range(n-l+1):
j = i + l - 1
if l == 2:
dp[i][j] = s[i] == s[j]
else:
dp[i][j] = s[i] == s[j] and dp[i+1][j-1]
if dp[i][j] and l > max_len:
max_len = l
start = i
return s[start:start+max_len]
13. Задача о подмассиве максимального произведения (Maximum Product Subarray)
Задача о подмассиве максимального произведения заключается в поиске непрерывного подмассива в одномерном массиве чисел с наибольшим произведением.
def max_product_subarray(nums):
n = len(nums)
max_prod = nums[0]
min_prod = nums[0]
max_so_far = nums[0]
for i in range(1, n):
temp = max_prod
max_prod = max(nums[i], max(nums[i] * max_prod, nums[i] * min_prod))
min_prod = min(nums[i], min(nums[i] * temp, nums[i] * min_prod))
max_so_far = max(max_so_far, max_prod)
return max_so_far
14. Самый большой прямоугольник на гистограмме
Задача «Самый большой прямоугольник в гистограмме» включает в себя поиск самого большого прямоугольника, который может быть сформирован на гистограмме, состоящей из прямоугольников разной высоты.
def largest_rectangle_area(heights):
n = len(heights)
left = [0] * n
right = [0] * n
stack = []
for i in range(n):
while stack and heights[stack[-1]] >= heights[i]:
stack.pop()
left[i] = stack[-1] if stack else -1
stack.append(i)
stack = []
for i in range(n-1, -1, -1):
while stack and heights[stack[-1]] >= heights[i]:
stack.pop()
right[i] = stack[-1] if stack else n
stack.append(i)
max_area = 0
for i in range(n):
max_area = max(max_area, heights[i] * (right[i] - left[i] - 1))
return max_area
15. Бросание яиц
Задача о бросании яиц состоит в том, чтобы найти минимальное количество попыток, необходимых для определения самого высокого этажа, с которого яйцо может быть сброшено, не разбиваясь.
def egg_drop(n, k):
dp = [[0] * (k+1) for _ in range(n+1)]
for i in range(1, n+1):
dp[i][1] = 1
dp[i][0] = 0
for j in range(1, k+1):
dp[1][j] = j
for i in range(2, n+1):
for j in range(2, k+1):
dp[i][j] = float('inf')
for x in range(1, j+1):
res = 1 + max(dp[i-1][x-1], dp[i][j-x])
dp[i][j] = min(dp[i][j], res)
return dp[n][k]
16. Подсчет битов
Задача подсчета битов заключается в том, чтобы найти количество единичных битов в двоичном представлении каждого числа от 0 до n.
def count_bits(n):
dp = [0] * (n+1)
for i in range(1, n+1):
dp[i] = dp[i >> 1] + (i & 1)
return dp
17. Идеальные квадраты
Задача о совершенных квадратах заключается в том, чтобы найти минимальное количество совершенных квадратных чисел, которые в сумме дают заданное число.
def num_squares(n):
dp = [float('inf')] * (n+1)
dp[0] = 0
for i in range(1, n+1):
j = 1
while j*j <= i:
dp[i] = min(dp[i], dp[i-j*j] + 1)
j += 1
return dp[n]
18. Раздел равной суммы подмножества (Partition Equal Subset Sum)
Проблема равной суммы подмножеств разделов включает в себя определение того, можно ли разбить данный набор на два подмножества так, чтобы сумма элементов в обоих подмножествах была одинаковой.
def can_partition(nums):
n = len(nums)
s = sum(nums)
if s % 2 != 0:
return False
target = s // 2
dp = [False] * (target+1)
dp[0] = True
for i in range(1, n+1):
for j in range(target, nums[i-1]-1, -1):
dp[j] |= dp[j-nums[i-1]]
return dp[target]
19. Самая длинная общая подстрока
Задача «Самая длинная общая подстрока» заключается в поиске самой длинной подстроки, общей для двух заданных строк.
def longest_common_substring(s1, s2):
m, n = len(s1), len(s2)
dp = [[0] * (n+1) for _ in range(m+1)]
max_len = 0
for i in range(1, m+1):
for j in range(1, n+1):
if s1[i-1] == s2[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
max_len = max(max_len, dp[i][j])
return max_len
22. Уникальные пути
Проблема уникальных путей включает в себя поиск количества уникальных путей из верхнего левого угла в нижний правый угол сетки m x n, по которым вы можете двигаться только вниз или вправо.
def unique_paths(m, n):
dp = [[0] * n for _ in range(m)]
dp[0][0] = 1
for i in range(m):
for j in range(n):
if i > 0:
dp[i][j] += dp[i-1][j]
if j > 0:
dp[i][j] += dp[i][j-1]
return dp[m-1][n-1]
23. Расстояние Левенштейна с помощью разрешенных операций
Задачу «Расстояние Левенштейна» можно расширить, если мы хотим разрешить только определенный набор операций редактирования, таких как вставка, удаление и замена.
def edit_distance_with_allowed_ops(s1, s2, allowed_ops):
m, n = len(s1), len(s2)
dp = [[0] * (n+1) for _ in range(m+1)]
for i in range(m+1):
dp[i][0] = i
for j in range(n+1):
dp[0][j] = j
for i in range(1, m+1):
for j in range(1, n+1):
if s1[i-1] == s2[j-1]:
dp[i][j] = dp[i-1][j-1]
elif allowed_ops.get((s1[i-1], s2[j-1])):
op_cost = allowed_ops[(s1[i-1], s2[j-1])]
dp[i][j] = min(dp[i-1][j] + op_cost[0], dp[i][j-1] + op_cost[1], dp[i-1][j-1] + op_cost[2])
else:
dp[i][j] = 1 + min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1])
return dp[m][n]
24. Проблема суммы подмножества
Проблема суммы подмножества включает в себя определение того, существует ли подмножество заданного набора целых чисел, которое в сумме дает заданную сумму.
def subset_sum(nums, target):
n = len(nums)
dp = [[False] * (target+1) for _ in range(n+1)]
for i in range(n+1):
dp[i][0] = True
for i in range(1, n+1):
for j in range(1, target+1):
if nums[i-1] <= j:
dp[i][j] = dp[i-1][j-nums[i-1]] or dp[i-1][j]
else:
dp[i][j] = dp[i-1][j]
return dp[n][target]
25. Самая длинная палиндромная последовательность
Задача «Самая длинная палиндромная подпоследовательность» включает в себя поиск самой длинной подпоследовательности заданной строки, которая является палиндромом.
def longest_palindromic_substring(s):
n = len(s)
dp = [[False] * n for _ in range(n)]
max_len = 1
start = 0
for i in range(n):
dp[i][i] = True
for l in range(2, n+1):
for i in range(n-l+1):
j = i + l - 1
if l == 2:
dp[i][j] = s[i] == s[j]
else:
dp[i][j] = s[i] == s[j] and dp[i+1][j-1]
if dp[i][j] and l > max_len:
max_len = l
start = i
return s[start:start+max_len]
25. Самый большой прямоугольник на гистограмме
Задача «Самый большой прямоугольник в гистограмме» включает в себя поиск самого большого прямоугольника, который может быть сформирован на гистограмме, состоящей из прямоугольников разной высоты.
def largest_rectangle_area(heights):
n = len(heights)
left = [0] * n
right = [0] * n
stack = []
for i in range(n):
while stack and heights[stack[-1]] >= heights[i]:
stack.pop()
left[i] = stack[-1] if stack else -1
stack.append(i)
stack = []
for i in range(n-1, -1, -1):
while stack and heights[stack[-1]] >= heights[i]:
stack.pop()
right[i] = stack[-1] if stack else n
stack.append(i)
max_area = 0
for i in range(n):
max_area = max(max_area, heights[i] * (right[i] - left[i] - 1))
return max_area
Уникальные пути 2
Задача «Уникальные пути II» — это разновидность задачи «Уникальные пути», в которой некоторые ячейки в сетке заблокированы и по ним нельзя пройти. Задача состоит в том, чтобы найти количество уникальных путей из верхнего левого угла в нижний правый угол сетки, где вы можете двигаться только вниз или вправо и не можете ходить по заблокированным ячейкам.
def unique_paths_with_obstacles(obstacle_grid):
m, n = len(obstacle_grid), len(obstacle_grid[0])
dp = [[0] * n for _ in range(m)]
if obstacle_grid[0][0] == 0:
dp[0][0] = 1
for i in range(m):
for j in range(n):
if obstacle_grid[i][j] == 0:
if i > 0:
dp[i][j] += dp[i-1][j]
if j > 0:
dp[i][j] += dp[i][j-1]
return dp[m-1][n-1]
Заключение
Динамическое программирование — это мощный инструмент, необходимый для решения множества сложных задач спортивного программирования. Алгоритмы, обсуждаемые в этом блоге, — лишь некоторые из многих проблем, которые можно решить с помощью динамического программирования. Освоив эти алгоритмы и поняв лежащие в их основе принципы, вы сможете стать более конкурентоспособным программистом и решать более сложные задачи.



Как вы относитесь к спортивному программированию?