Условие задачи
Вы – расхититель гробниц. Нужно пройти над пропастью по лестнице, охраняемой Сфинксом. Как водится, Сфинкс задает загадку. Решите задачу неверно – и лестница провалится в пропасть, когда вы по ней пойдете.
Условие задачи. Строительными блоками лестницы являются балки с квадратным сечением, соединенные по три таким образом, что срез имеет форму тримино (как у правой фигуры на рисунке). Для каких n можно составить лестницу из таких тройных блоков, если n – число квадратных балок в ее основании? На рисунке приведено поперечное сечение лестницы для n = 8.
Другими словами, какие лестничнообразные фигуры с основанием из n квадратов можно разрезать нацело на тримино?
Решение – в следущей задаче.
Эта задача – пятнадцатый эпизод нашего сериала головоломок. После описания задачи идёт ответ на предыдущую – алгоритмическую задачу о прыгающих лягушках. Ответ и новая задача будут опубликованы в 14:00 в субботу.
Решение алгоритмической задачи о лягушках
Если вы не решали эту задачу, прежде чем читать приведенный ниже текст, прочитайте условие и попробуйте решить самостоятельно!
Решение. Движение лягушки сводится либо к прыжку через лягушку противоположного вида, либо к переходу лягушки на соседнюю пустую клетку. Таким образом, если мы найдем общее количество прыжков и переходов, мы узнаем общее количество ходов.
Прыжок – единственный способ, которым лягушки противоположного вида могут преодолеть друг друга. Мы сталкивались с этим ранее в предыдущих задачах: получается, что для того, чтобы преодолеть друг друга, им необходимо совершить n2 прыжков в случае n настоящих и n виртуальных лягушек.
Сдвиг. Рассмотрим далее ситуацию для лягушек одного вида. Мы знаем, что они не могут перепрыгивать друг через друга. Первая лягушка переместится на n + 1 клеток и окажется в ячейке n + 2, вторая лягушка передвинется на n + 1 клеток до ячейки n + 3, и т. д. Чтобы оказаться в нужной позиции, вместе все лягушки одного вида должны переместиться на n (n + 1) клеток. Аналогично должны сделать их виртуальные аналоги. То есть все эти реальные и виртуальные земноводные переместятся на 2 n (n + 1) клеток. Поскольку один прыжок охватывает две ячейки, и их n2, количество сдвигов должно составить 2n (n + 1) – 2n2 = 2n.
Алгоритм. Существует два симметричных алгоритма для решения головоломки: один начинается со сдвига крайней к пустой ячейки настоящей лягушки, другой – со сдвига виртуальной. Опишем первый. Алгоритм может быть получен методом грубой силы: его ходы определены однозначно, потому что альтернативные ходы приводят к очевидным тупиковым ситуациям. В частности, когда есть выбор между сдвигом и прыжком, должен быть сделан прыжок.
Ниже приведены алгоритмы для n = 2 и n = 3 соответственно. Настоящие лягушки обозначены T, виртуальные – F.
1 TT_FF
2 T_TFF
3 TFT_F
4 TFTF_
5 TF_FT
6 _FTFT
7 F_TFT
8 FFT_T
. FF_TT
1 TTT_FFF
2 TT_TFFF
3 TTFT_FF
4 TTFTF_F
5 TTF_FTF
6 T_FTFTF
7 _TFTFTF
8 FT_TFTF
9 FTFT_TF
10 FTFTFT_
11 FTFTF_T
12 FTF_FTT
13 F_FTFTT
14 FF_TFTT
15 FFFT_TT
. FFF_TTT
Головоломка может быть легко обобщена на случай с m и n лягушками разных видов. Общее количество необходимых ходов равно mn + m + n, из которых mn – количество прыжков, а m + n – число сдвигов.
Ответ: для 3 лягушек с каждой стороны достаточно 15 ходов.
Ответ на вопрос со звёздочккой: Для m и n лягушек достаточно mn + m + n ходов.
Как ответили читатели Библиотеки программиста? Сам ответ о числе переходов первым дал пользователь wil4, но без указания решения:
15 для n=3
Первым ответ с решением, но с чуть большим числом ходов дал пользователь mr.fantazylight:

В комментариях к решению задачи мы обсудили, откуда берутся два лишних хода.
Программное решение, находящее алгоритм для любого m и n, реализовал на С++ пользователь krotbsod. Вот пример для m = 3 и n = 5:
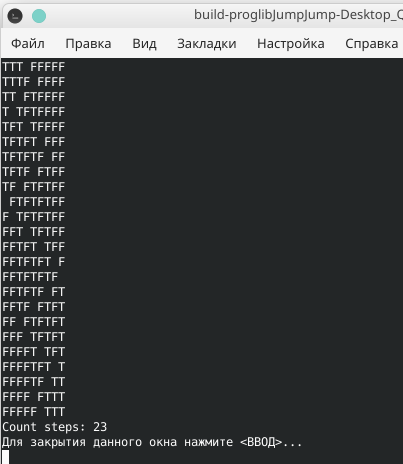
Автор решения krotbsod будет рад получить комментарии относительно кода: https://pastebin.com/Qm3Ru08L.
#include <iostream>
#include <cstring>
using namespace std;
//!!! P.S. Некоторые проверки в программе не выполняются, для упрощения восприятия
/**
* @brief Генерируем лягушек
* @param frogs Указатель на массив с лягушками [m + n + 1] размерности
* @param m T лягушек
* @param n F лягушек
**/
void generateFrogs(char *frogs, const int m , const int n) {
int count = m + n + 1;
memset(frogs, ' ', count);
for(int i = 0; i < m; i++) {
frogs[i] = 'T';
}
for(int i = m + 1; i < count; i++) {
frogs[i] = 'F';
}
}
/**
* @brief Заданные шаблоны поведения лягушек возле свободной ячейки
*/
struct Patterns{
public:
// T1 <-- Цифра - количество шагов
// ^
// |
// Символ - тип лягушки
/**
* @brief Задаем шаблоны в конструкторе структуры и записываем указатели в m_list
*/
Patterns() {
m_list[0] = "TF FT"; // T2
m_list[1] = "FT TF"; // F2
m_list[2] = "FF FT"; // F1
m_list[3] = "TT TF"; // F2
m_list[4] = "FF TF"; // F2
m_list[5] = "TT FT"; // T1
m_list[6] = "TF FF"; // T2
m_list[7] = "FT TT"; // T1
m_list[8] = "FT FF"; // F1
m_list[9] = "TF TT"; // T2
m_list[10] = "FT FT"; // F1 or T1
m_list[11] = "TF TF"; // lock
m_list[12] = "TT FF"; // F1 or T1
m_list[13] = "FF FF"; // F1;
m_list[14] = "TT TT"; // T1;
m_list[15] = "FF TT"; // done
}
/**
* @brief Возвращает указатель на заданный шаблон.
* Нужна лишь для итеративного поиска.
* @param num Номер шаблона в m_list
* @return Указатель на заданный шаблон
*/
const char *pattern(const int &num) {
// Проверку не стал делать, для упрощения восприятия
return m_list[num];
}
/**
* @brief Возвращает число шаблонов
* @return Число шаблонов
*/
int size() {
return m_size;
}
private:
static const int m_size = 16;
// Массив с указателями на массивы шаблонов
const char *m_list[m_size];
} frog_patterns;
/**
* @brief Получение текущего состояния (шаблона) в массиве с лягушками
* @param currentPattern Указатель на формируемый массив для записи в него шаблона
* @param frogs Указатель на массив с лягушками
* @param count Размер массива с лягушками
* @param iter Текущее положение пробела
*/
void getCurrentPattern(char *currentPattern, char *frogs, const int &count, const int &iter) {
//Задаем шаблон текущего положения для последующего сравнения с заданными шаблонами
memcpy(currentPattern, &frogs[iter - 2], 5); // dangerous !!! Опасно, выходим за рамки заданного массива. Но работает
// Задаем МНИМЫХ лягушек в текущий шаблон для последующего сравнения с заданными шаблонами.
// Когда символ пробела находится с краю, например: 'FF |' или '|T FF' (где | край массива)
// То приходим в несколько неодназначную ситуацию.
// Проще всего этого избежать добавив МНИМЫХ лягушек в шаблон для сравнения.
// Для конечных точек характеры следующие МНИМЫЕ лягушки: Для начального положения(крайнего левого предела) характерна мнимая F
// Для последнего положения(крайнего правого предела) характерна мнимая T
// P.S. МНИМЫЕ лягушки на то и мнимые, они ни как не дополняют исходный массив, они лишь заполняют шаблон для сравнения.
if(iter == 0) {
currentPattern[0] = 'F';
currentPattern[1] = 'F';
}
if(iter == 1) {
currentPattern[0] = 'F';
}
if(iter == (count - 1)) {
currentPattern[3] = 'T';
currentPattern[4] = 'T';
}
if(iter == (count - 2)) {
currentPattern[4] = 'T';
}
}
/**
* @brief Перемещение лягушки на место пустой ячейки
* @param frogs Указатель на массив с лягушками
* @param iter Текущее положение пробела
* @param type Тип лягушки
* @param step Шаг для перемещения лягушки
*/
void moveFrog(char *frogs, const int &iter, const char &type, const int &step) {
if(type == 'F') {
frogs[iter] = frogs[iter + step];
frogs[iter + step] = ' ';
}
if(type == 'T') {
frogs[iter] = frogs[iter - step];
frogs[iter - step] = ' ';
}
}
/**
* @brief Основной цикл сравнения состояний
* @param frogs Указатель на массив с лягушками
* @param m T лягушек
* @param n F лягушек
* @param iter Текущее положение пробела
* @return Возвращает 1, если перемещение всех лягушек завершено. В остальных случаях 0.
*/
int move(char *frogs, const int &m , const int &n, const int &iter) {
int count = m + n + 1;
char currentPattern[5];
memset(currentPattern, ' ', 5);
getCurrentPattern(currentPattern, frogs, count, iter);
// Проходим по всем заданным шаблонам
for(int i = 0; i < frog_patterns.size(); i++) {
// Сравниваем
int rescmp = memcmp(currentPattern, frog_patterns.pattern(i), 5);
if(rescmp == 0) {
// При совпадении перемещаем
switch (i) {
case 0:
moveFrog(frogs, iter, 'T', 2); // T2
break;
case 1:
moveFrog(frogs, iter, 'F', 2); // F2
break;
case 2:
moveFrog(frogs, iter, 'F', 1); // F1
break;
case 3:
moveFrog(frogs, iter, 'F', 2); // F2
break;
case 4:
moveFrog(frogs, iter, 'F', 2); // F2
break;
case 5:
moveFrog(frogs, iter, 'T', 1); // T1
break;
case 6:
moveFrog(frogs, iter, 'T', 2); // T2
break;
case 7:
moveFrog(frogs, iter, 'T', 1); // T1
break;
case 8:
moveFrog(frogs, iter, 'F', 1); // F1
break;
case 9:
moveFrog(frogs, iter, 'T', 2); // T2
break;
case 10:
moveFrog(frogs, iter, 'F', 1); // F1 or T1
break;
case 12:
if((m % 2) == 0) {
moveFrog(frogs, iter, 'T', 1);
} else {
moveFrog(frogs, iter, 'F', 1);
}
//moveFrog(frogs, iter, 'F', 1); // F1 or T1 //if m is even use T1
break;
case 13:
moveFrog(frogs, iter, 'F', 1);
break;
case 14:
moveFrog(frogs, iter, 'T', 1);
break;
case 15:
return 1;
break;
}
}
}
return 0;
}
/**
* @brief Запуск цикла алгоритма
* @param m T лягушек
* @param n F лягушек
*/
void jumpAlg(const int m , const int n) {
int count = m + n + 1;
char frogs[count + 1]; // +1 чтобы добавить символ \0 в конец, для корректного вывода через printf
frogs[count] = '\0'; // тут и добавим
generateFrogs(frogs, m, n); // Генерируем массив с лягушками
int counter = 0;
while(true) {
printf("%s\n", frogs);
int ret = 0;
for(int iter = 0; iter < count; iter++) {
// При нахождении пробела, входим в Основной цикл сравнения состояний
if(frogs[iter] == ' ') {
ret = move(frogs, m, n, iter);
break;
}
}
if(ret == 1) {
printf("Count steps: %d\n", counter);
break;
}
counter++;
}
}
int main()
{
//
// T, F
jumpAlg(3, 5);
return 0;
}
Спасибо, что присылаете в комментарии свои ответы и решения!

















Комментарии
3 k - (1) (k % 2) для всех натуральных чисел. Получаем мы длинну основания пирамиды. Логика такая: Вычисляем общее количество кубиков для каждого к. Исключаем те что делятся на 3 с остатком . Замечаем, что только чётные можно застроить. Исключаем нечётные. Пытаемся найти закономерность. (2,6,8,12,14,18,20,24,26,30...) Выясняем что для чётных к, n = 3 к, а для не чётных k, n = 3 к - 1. Не уверен в полноте, но вроде как всё сходится.
Почему знаки умножения не отображаются.
Пока неполно. Для нечетных k тоже будет работать. Подробный ответ с иллюстрациями я описал здесь. https://proglib.io/p/sobesedovanie-i-sem-gnomov-zadachi-s-intervyu-v-it-kompaniyah-2020-02-22
Как вариант N = 2 * k + (3 - (k // 2)). Где // результат деления с отбрасыванием целой части.
mod(2n-1, 3)>0 and n > 2
Если мы подставим n=3, mod(5, 3) > 0, но для n=3 решения разрезания на тримино нет.
Могут только сказать, что всё гораздо проще.
Ну думаю решил. Для чётных выслеживается зависимость: r=((N^2)/2+N/2) mod 3 (Можно упростить до r=((N^2 + N)/2) mod 3). Если остаток r равен 0, то N будет верным основанием башни. Для нечетных могу ошибаться, но выслеживается простая зависимость: r=N^2 mod 3, где N=3 исключение.
Сами числа теперь и верны, и полны, но зависимость можно описать немного проще = )
Неужели это верно для всех простых N которые соответствуют условию r=n(n+1)/2 mod 3, где остаток r должен быть равен 0? Исключение из правил числа 3 и 5...
Можно так сформулировать правило, что про несколько исключений в нем говорить не придется. Но вы уже очень близко.
Верно? Если да, то напишу условие нахождения...
Те, что указаны – верные, но пока перечислены не все.
Хорошо, можно тогда уточнить условие? Лестница обязательно должна иметь последнюю верхнюю ступень или нет? Просто не совсем понятно как решение может быть для нечетных чисел...
Да, лестница всегда как на картинке. Фигуры тримино могут поворачиваться как угодно, заполняя собой квадраты "лестницы".
Как минимум - решения быть не может там, где количество ячеек не кратно 3 (в основании 2, 5, 8,... блоков по 2 ячейки) для 1 - решение очевидно, для 3 и 4 - подобрано
ставлю на все, кроме 3^x-1 для x>0, хотя доказать пока не могу
Задача в том, чтобы найти для n квадратов в основании, а не n тримино в основании. То есть вы нашли решения для n, равных 2, 6 и 8, а не одному, трём и четырём (перечитайте, пожалуйста, условие). Но вы на верном пути.
Ответ: a+6*b, где а={2,6,9,11}, b - целое неотрицательное {0,1,2,3,...}. Решение чуть позже оформлю.
Фотка не отправляется :(
Для начала представим все n в таблице с 6ю колонками, записав их последовательно. В первой строке 1,2,3,4,5,6. Во второй 7,8,9,10,11,12. И т.д. Для n=1 число клеток не делится на 3. Методом индукции можно убедиться, что, если для n число клеток пирамиды не делится на 3, то и для (n+3) число клеток не будет делиться на 3. Действительно, если к пирамиде для n добавить 3 ряда в основание, то число клеток всей пирамиды увеличится на число, делящееся на 3. В итоге результат не будет делится на 3. Из этого правила вытекает, что n в 1м и 4м столбцах не имеют решений. Легко убедиться, что нет решений для чисел 3 и 5, но есть решения для 2,6,9 и 11. Можно убедиться, что если есть решение для некоторого n, то есть решение для (n+6). Действительно, добавим к пирамиде для n в основание 6 рядов. Добавку можно разделить на 2 фигуры: пирамиду для 6 слева (которая имеет решение) и прямоугольник 6m. Очевидно, что эта вторая фигура хорошо делится на прямоугольники 23, которые имеют решение. Таблицу чисел, для которых могут быть найдены решения можно представить в виде: х 2 х х х 6 х 8 9 х 11 12 х 14 15 х 17 18 х 20 22 х 23 24 И т.д. Итого ответ: n=a+b*6, где a={2,6,9,11}, b={0,1,2,3,...}
К сожалению моя табличка с 6ю столбцами предстала в виде строки.
23 это 2х3
Из самого доказательства понятен и алгоритм разделения любой пирамиды на тримино, если для нее есть решение.
Верно, только ответ можно записать в более краткой форме, не используя указанного ряда значений, заметив закономерность в общем ряду чисел {6, 8, 9, 11, 12, 14, 15...}. Для n=2 нам сами разрезания не понадобятся, фигура уже «разрезана». А вот все остальные, что действительно разрезаются, можно описать, не вводя перечислительного множества.
mod(n,3)<>1, n > 5
Любое четное n больше 4?
Пока неверно, лестница обрушится. Например, для n=2 условие выполняется очевидным образом. И нечетные решения тоже могут быть.