Почему 0,999 равняется 1, и в чём проблема дня рождения?

Почему 0,999... равняется 1?!

«Чуть-чуть» не считается, за исключением метания подковы, бросков ручной гранаты и… математики?

Что?! Это несерьёзно, да?

Советуем раньше времени не разочаровываться в математической точности, потому что впервые в истории близость значения на самом деле математически точна!

Сейчас вы узнаете, как с помощью базовой математики продемонстрировать друзьям то, что периодическая десятичная дробь 0,999… в действительности равняется 1.

Да, вы всё правильно поняли. Покажем, что это правда, без лишних премудростей. Никаких вычислений, никаких пределов и каких бы то ни было продвинутых концепций. Итак, начнём!

Как перевести периодические десятичные дроби в обыкновенные

Часто люди не понимают, что можно легко записать любую периодическую десятичную дробь в виде обыкновенной.

Итак, вот, что понадобится.

Если у вас одночисловое бесконечное значение, напишите повторяющуюся цифру над знаменателем 9. Таким образом, мы получим:

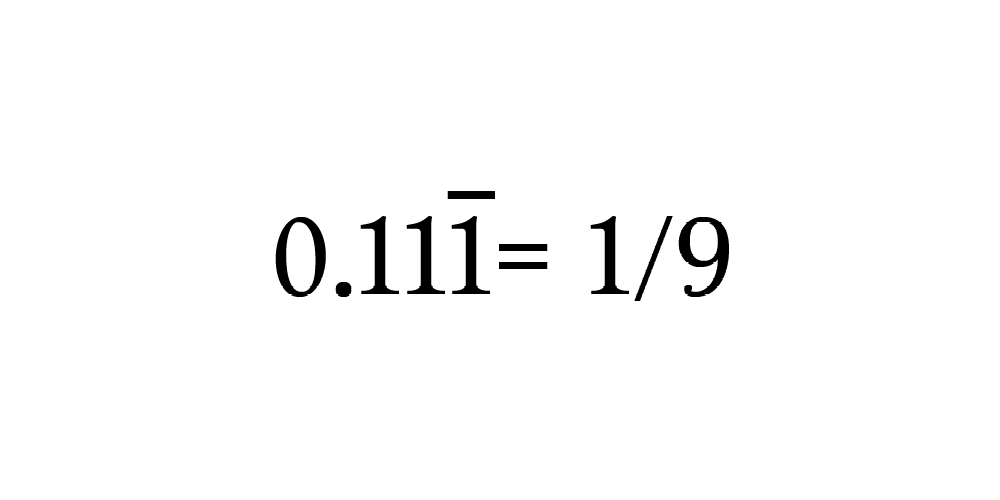
Если в дроби чередуются 2 числа, запишите повторяющиеся цифры в числитель над 99.

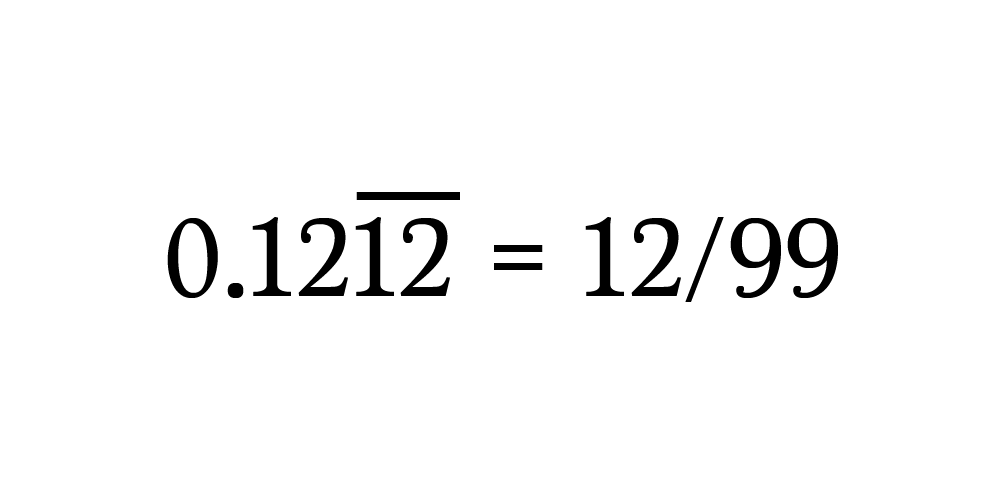
При повторении трёх чисел в значении повторяющиеся цифры записывайте над знаменателем 999.

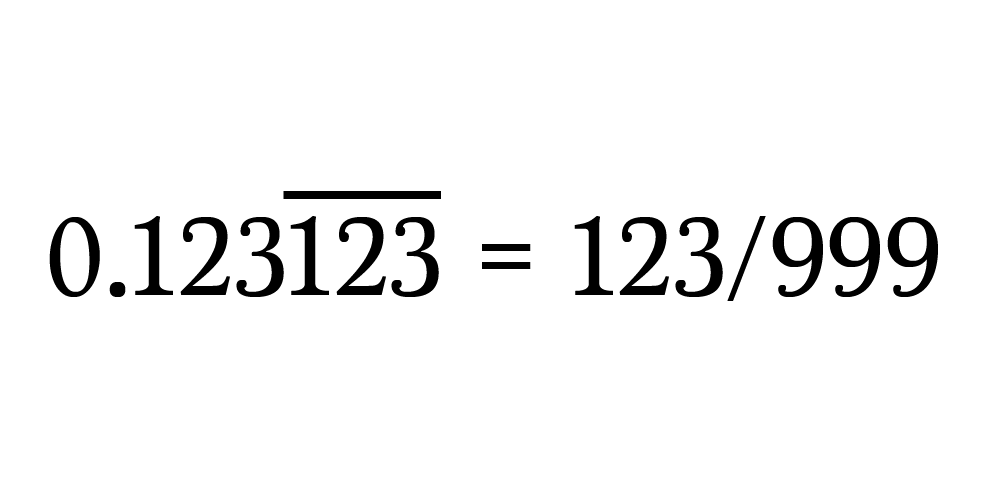
Заметили закономерность?

С учётом N повторяющихся цифр формула обретает вид:

Демонстрация равенства 0,999... и 1

Ладно, поехали! Начните с приравнивания 0,999... эквивалентной дроби.

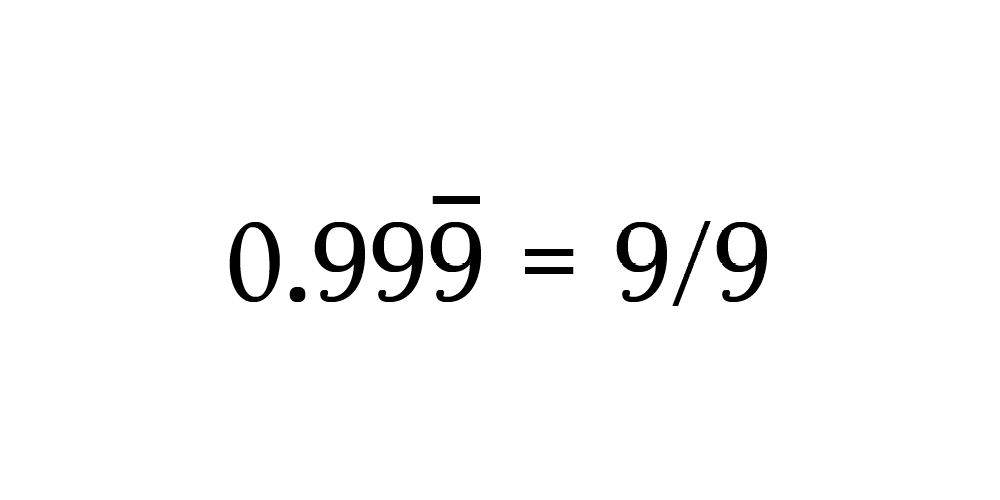
Конечно, 9 ÷ 9 = 1. Поэтому получаем:

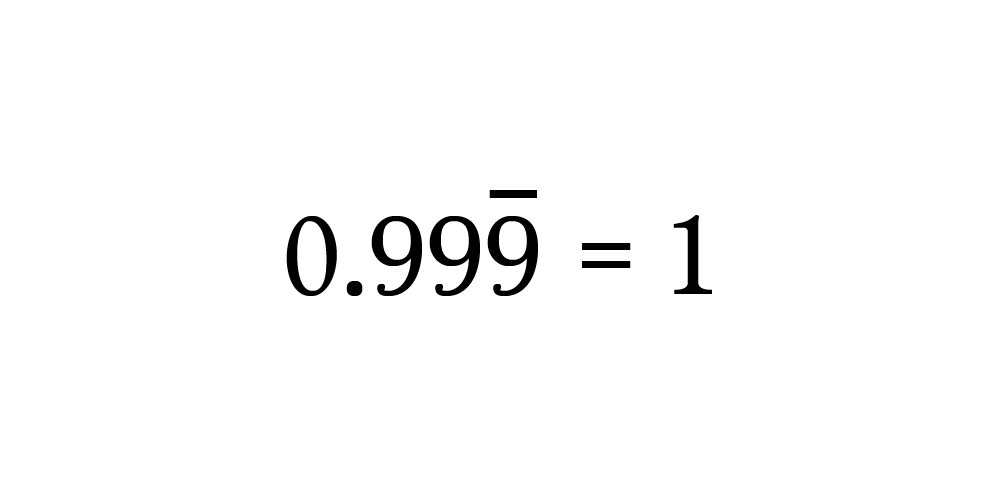
Здесь, пожалуй, закончим. Коротко и ясно.

Всё ещё не убеждены?

До сих пор удивляетесь, как это может быть правдой? Понимаем, ведь это совершенно противоречит здравому смыслу и будоражит разум.

Предположим, что добавление девяток в конец числа 0,999... не только больше и больше приближает значение к 1, но и делает его равным 1.

Вот ещё один способ посмотреть на это.

1/3 равно 0,33333… и 2/3 равно 0,66666…, поэтому 1/3 + 2/3равняется0,333 +0,6666…, верно?

Суммируйте обе стороны и снова получите, что...

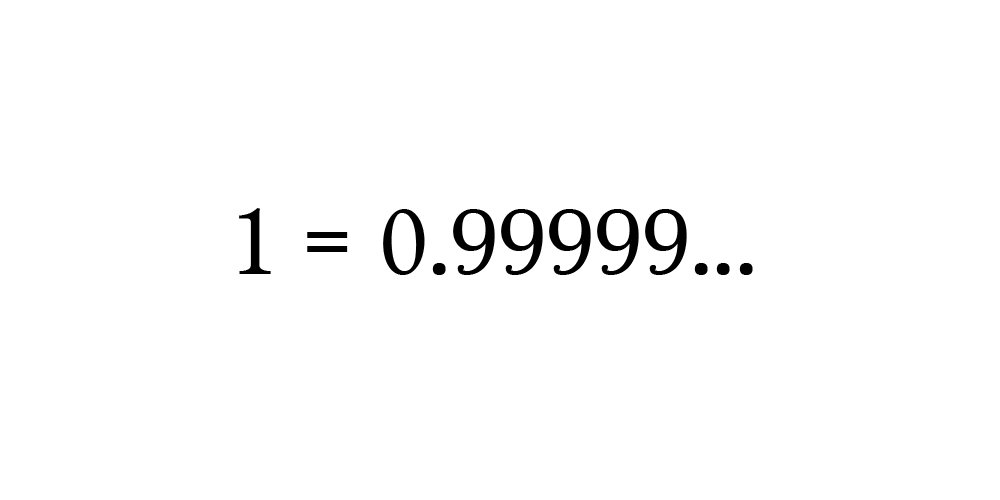
Любители математики, наверное, сейчас немного разочаровались, потому что это слишком легко и, как говорят в математическом мире, тривиально.

Слышу вас и тоже временами тоскую по математике. Все же задержитесь еще на немного и вы увидите, почему вышеописанная схема актуальна для бесконечных последовательностей. Вы наверняка знакомы с некоторыми замысловатыми тонкостями математики, которые мы не собирались сегодня использовать, но, кажется, придётся, ведь это будет стоить того.

Метод бесконечных последовательностей

Начнём с разложения значения 0,999… на разряды. Вспомните, как учитель в начальной школе объяснял разрядное значение числа и говорил что-то вроде:

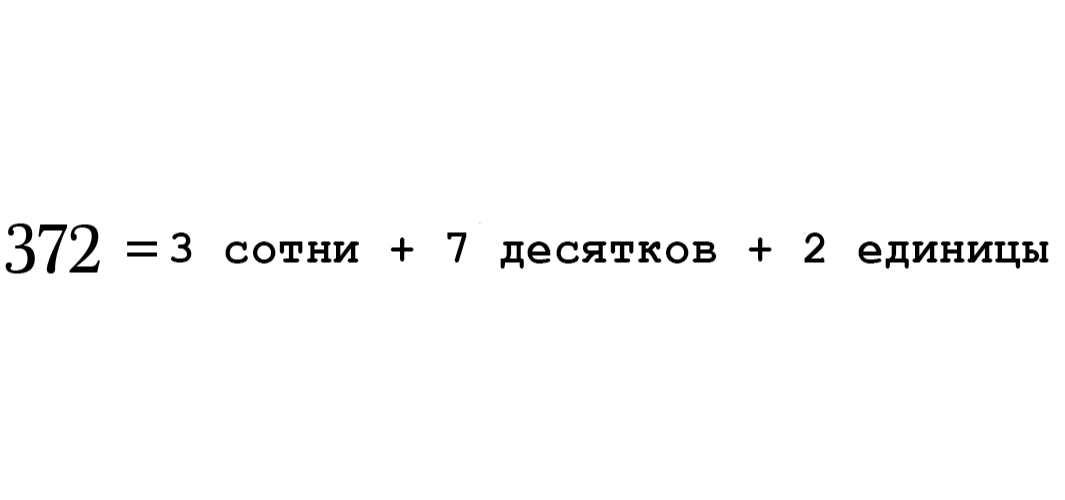
Напишем 0,999... таким же образом, начиная примерно так:

Или в виде дроби:

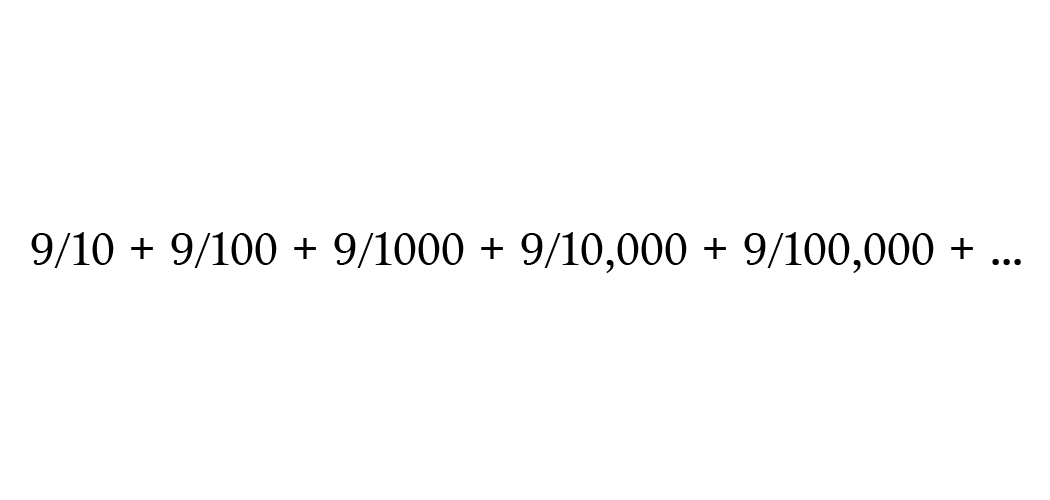
Если сложим первые 5 значений, то получим 0,99999, и, продолжая представлять дробь в десятичной форме, будем делать это до бесконечности и получим точное значение 0,999...

Выписать десятичное разложение до бесконечности вручную невозможно, поэтому воспользуемся сокращением.

Сначала вынесем 9 за скобки.

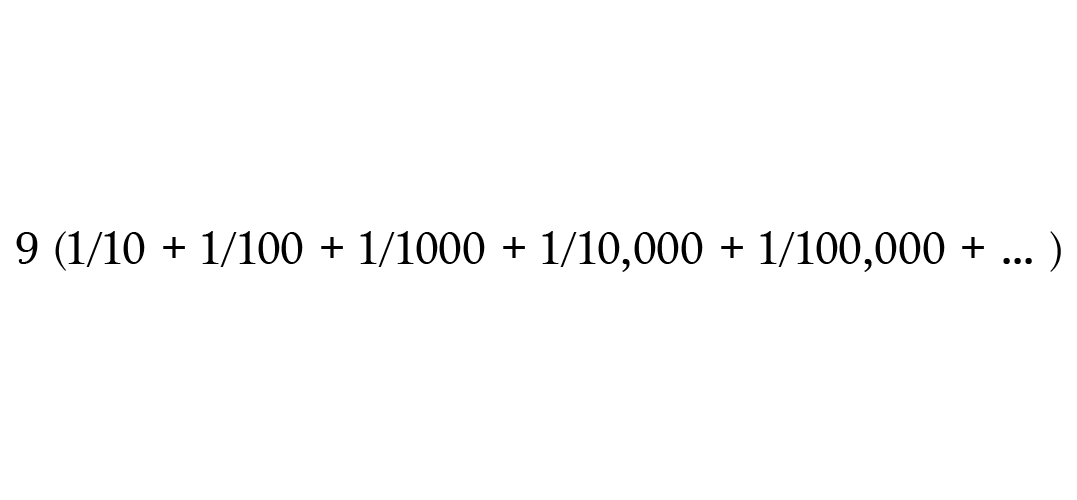
Затем перепишем знаменатели в виде 10 в степени.

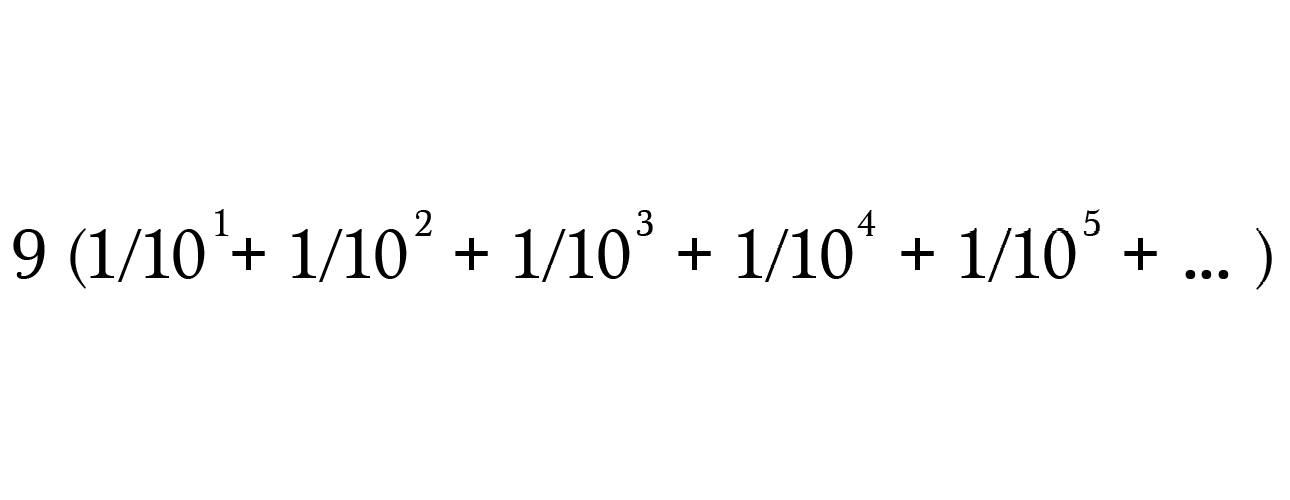
Теперь используем сигма-нотацию для представления бесконечной суммы.

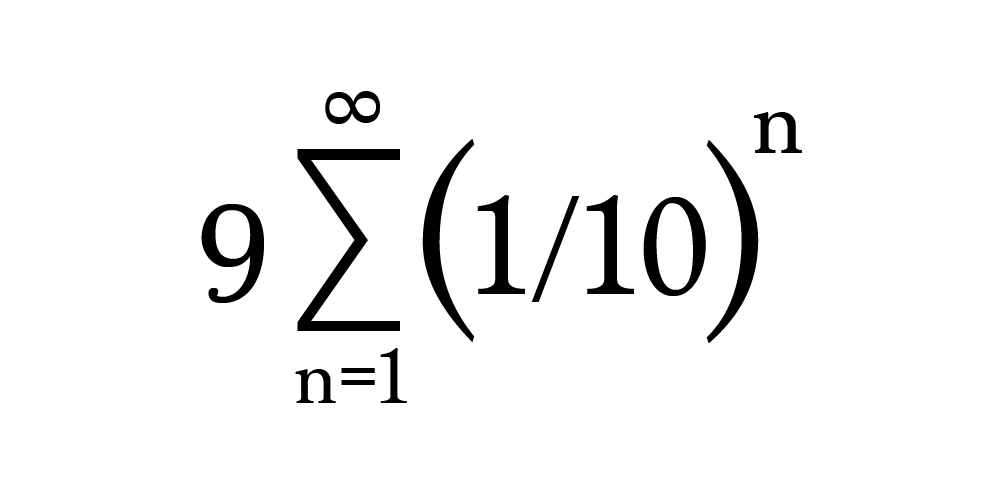
Дополнительное примечание к сигма-нотации: если вы новичок в сигма-нотации, позвольте рассказать об этом. Греческая буква ∑ (сигма) используется в математике для обозначения многократного сложения.

Первое значение при суммировании образуется путём подстановки первого указанного значения для n, которое можно найти под символом ∑. В этом случае значение равно n = 1, поэтому получаем (1/10)¹.

Чтобы отыскать следующее значение, нужно взять следующее целое число, n = 2, для получения (1/10)². Затем подставляйте n = 3, чтобы получить (1/10)³ , и так далее. Продолжайте делать это, пока не доберётесь до значения над символом ∑. В нашем случае это бесконечность, поэтому завершения нет.

И, конечно же, все эти образованные значения складываются вместе. В нашем случае их сумма затем умножается на 9.

Думать о числах в нашей последовательности можно и по-другому: каждый последующий член получается умножением предыдущего на знаменатель прогрессии.

Это означает, что у нас есть геометрическая прогрессия, которая сходится к a/(1 - r), где a – первое значение в ряду, а r – число-множитель для получения следующего члена.

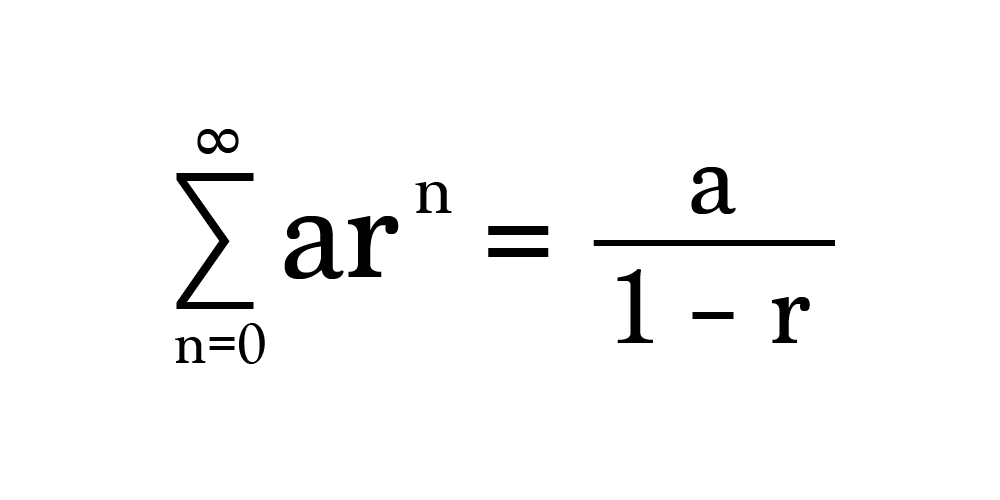
Сходимость означает, что последовательность будет всё приближаться и приближаться к конкретному значению, поскольку вы добавляете всё больше и больше членов в ряд. Последовательность становится бесконечно близкой к значению сходимости. В бесконечном масштабе сходимость превращается в равенство.

В нашем случае начинаем с 1/10 и каждый раз умножаем на 1/10, так что a и r = 1/10.

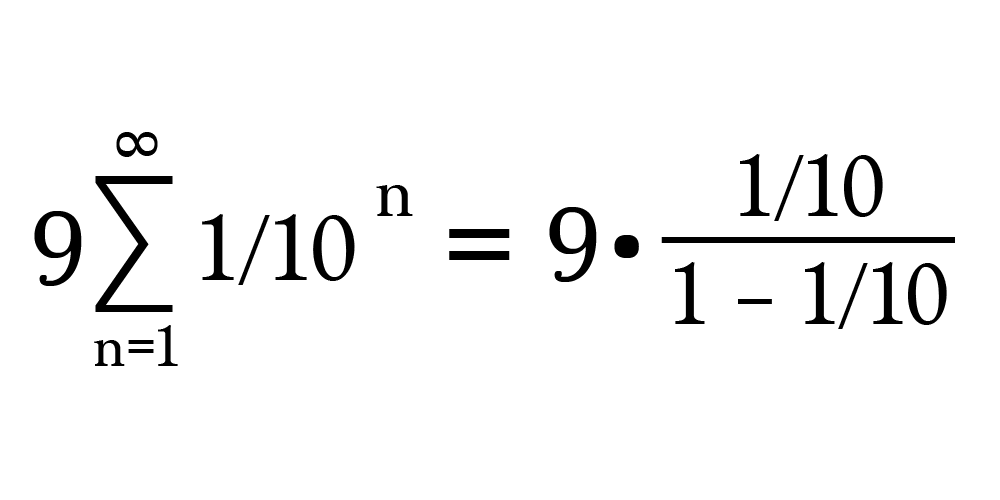
Завершим арифметические операции с правой стороны.

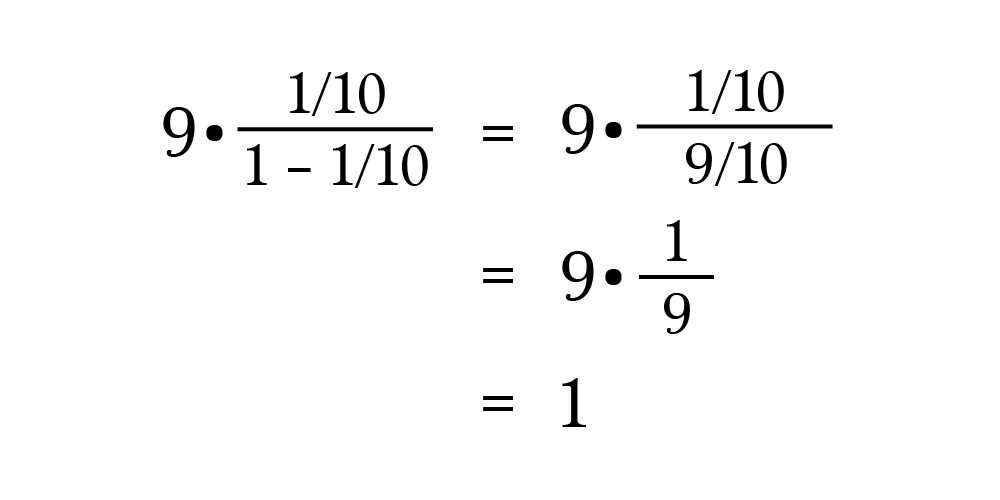
Теперь мы доказали, что 0,999… сходится к или равняется 1.

Заключительные мысли

Если это кажется нелепым, то всё в порядке! Вы знаете, что два разных числа должны на самом деле быть разными числами. Противоречащий здравому смыслу характер этой проблемы присущ странности, которая сопровождает работу с бесконечностью.

Даже в такой простой проблеме, как эта, вы выходите за границы осязаемого для человеческого сознания в масштаб за пределами нашего понимания. Как конечные существа, мы хватаемся за понимание концепции бесконечности или вечности, но никогда не сможем по-настоящему испытать её. Это означает, что часто вещи, правдивые для нашего конечного мира, ведут себя по-другому на бесконечном уровне.

Принятие перехода от легкодоступной и воспроизводимой математики к тому, что можно проверить и представить только в наших умах, – часть красоты и чуда науки.

Так что не принимайте сегодняшний урок близко к сердцу.

Пусть некий слой тумана останется между вами и полным пониманием. Пусть мозг взрывается от факта, что бесконечность ведёт себя странно. И пусть это вызывает страстную жажду исследования и, прежде всего, более углубленного изучения математики.

Проблема дня рождения в реальной жизни

Впервые я услышала эту задачу на курсе математической статистики 300-го уровня в небольшом университете на Тихоокеанском северо-западе. В классе было 30 студентов, и профессор поспорил, что как минимум у двоих один и тот же день рождения.

Затем он попросил всех назвать свой день рождения. Когда подошла моя очередь, я объявила дату рождения как «два в кубе, три в кубе», что заставило класс рассмеяться, поскольку наш высокоинтеллектуальный профессор завис на некоторое время, прежде чем расшифровать дату.

В любом случае, как он и предсказывал, ещё не добрались до последнего студента, а пара совпадающих дней рождения нашлась.

Так как же ему повезло найти соответствующую пару?

Разминка

Ограничение: ради простоты будем игнорировать возможность рождения 29 февраля.

Начнём с простого примера, чтобы размять наш мозг:

Какова вероятность того, что у двух человек одинаковый день рождения?

Человек А родился в любой день года, так как он первый, кого спрашиваем. Вероятность рождения в любой день года составляет 1 или 365/365.

Поскольку человек B должен родиться в тот же день, что и человек A, его вероятность составляет 1/365.

Мы хотим, чтобы оба события произошли, поэтому перемножаем вероятности:

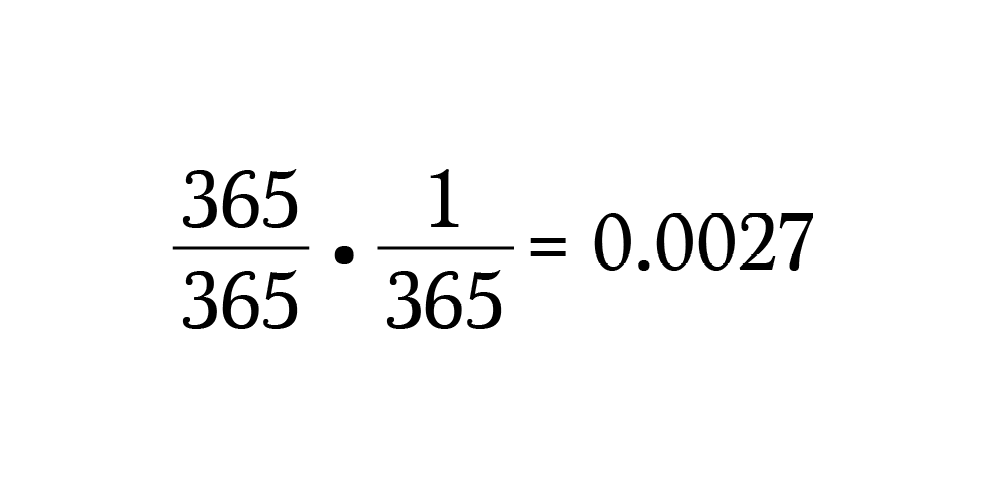
Таким образом, с вероятностью 0,27% вы подойдёте к незнакомцу и обнаружите, что его день рождения совпадает с вашим. Негусто.

Но что насчёт большей группы?

Какова вероятность, что по крайней мере у 2 из 4 человек одинаковый день рождения?

Чтобы решить эту проблему, придётся вычислить все следующие вероятности:

• у А и В одинаковый день рождения;
• у А и С совпадает день рождения;
• у D и A одинаковый день рождения; 
• у B и C одинаковый день рождения; 
• у B и D один и тот же день рождения;
• у C и D одинаковый день рождения; 
• у A, B и C одинаковый день рождения;
• у B, C и D одинаковый день рождения; 
• у C, A и D одинаковый день рождения; 
• у A, B и D одинаковый день рождения; 
• у A, B, C и D одинаковый день рождения.

Фу, как много расчётов! Представьте себе, сколько вероятностей пришлось бы рассчитать на класс из 30 студентов!

Должен быть способ получше...

Лучший способ – хитрость с дополнением

Самый простой способ вычислить что-то среди гигантиллиона вероятностей – посмотреть на проблему под другим углом.

Какова вероятность того, что никто не разделяет один и тот же день рождения?

Это альтернативное упражнение полезно, потому что представляет собой противоположность нашей первоначальной проблеме (то есть дополнение). Исходя из теории вероятности, мы знаем, что сумма всех возможных результатов – то есть выборочное пространство – всегда равна 1 или 100% вероятности.

Поскольку вероятность того, что по крайней мере у 2 человек одинаковый день рождения и вероятность отсутствия одинакового дня рождения, покрывают все возможные сценарии, сумма их вероятностей равна 1.

Или эквивалентно:

Ура! Это будет намного легче рассчитать.

Расчёт

Потрясающе! Мы наконец-то готовы выяснить, насколько безопасную ставку сделал профессор.

Определим вероятность того, что ни у кого из 30 человек день рождения не повторяется.

Разбиваем расчёт на последовательные операции:

• Первый студент может родиться в любой день, поэтому назначаем ему вероятность 365/365. 
• Следующий студент теперь ограничен 364 возможными днями, поэтому вероятность второго студента составляет 364/365. 
• Третий студент может родиться в любой из оставшихся 363 дней, то есть 363/365.

Этот шаблон продолжается, и у нашего последнего студента вероятность составляет 336/365 (365 – 29 дней, так как ученики до него израсходовали 29 потенциальных дней).

Снова перемножьте все 30 вероятностей между собой:

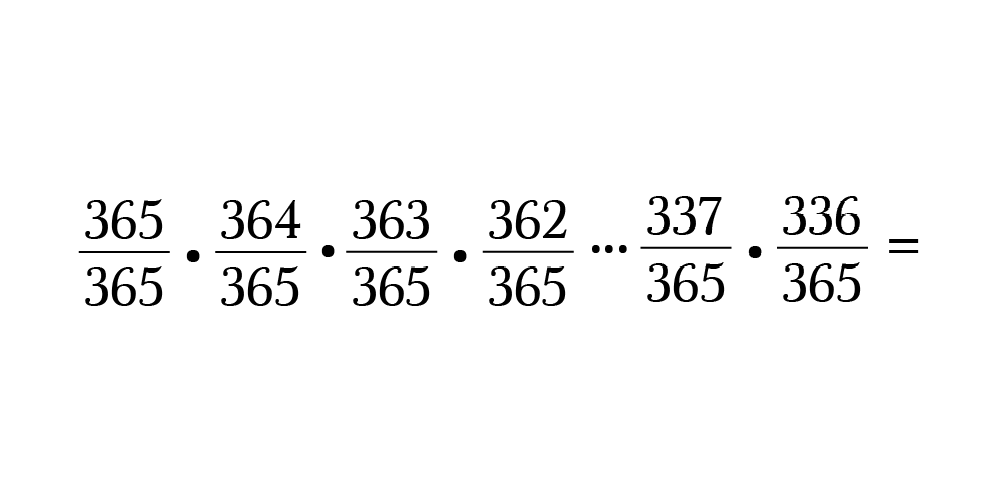
Держитесь! Вышло чуточку грязно. Дальше подправим.

Поскольку знаменатель – помноженное само на себя тридцать раз число 365, перепишем его следующим образом:

Используем факториалы (символически: !) для дальнейшей очистки этого расчёта.

С использованием факториала 365! будет равно произведению всех убывающих целых чисел с 365 до 1. Нам нужно произведение целых чисел только с 365 до 336, поэтому убираем посторонние числа делением 365! на 335!.

Примечание: если это приводит вас в замешательство, попробуйте меньшее значение, например, 5!/3! = 5 • 4 • 3 • 2 • 1/3 • 2 • 1. Обратите внимание на 3 • 2 • 1 в числителе и знаменателе. Они «сокращаются» и превращают 5!/3! = 5 • 4.

Собрав всё это вместе, получим выражение, которое можно легко ввести в инженерный калькулятор:

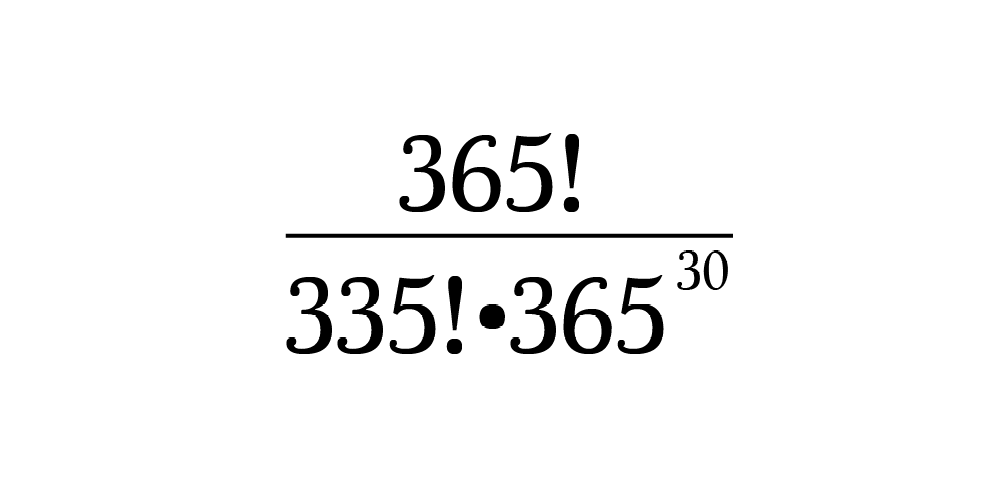
Результат составляет 0,294 или 29,4% вероятности того, что ни у кого в классе нет одинакового дня рождения. Конечно, нам нужно дополнение, поэтому вычтем значение из 1, чтобы определить вероятность того, что во всяком случае у 2 студентов в группе из 30 человек дни рождения совпали.

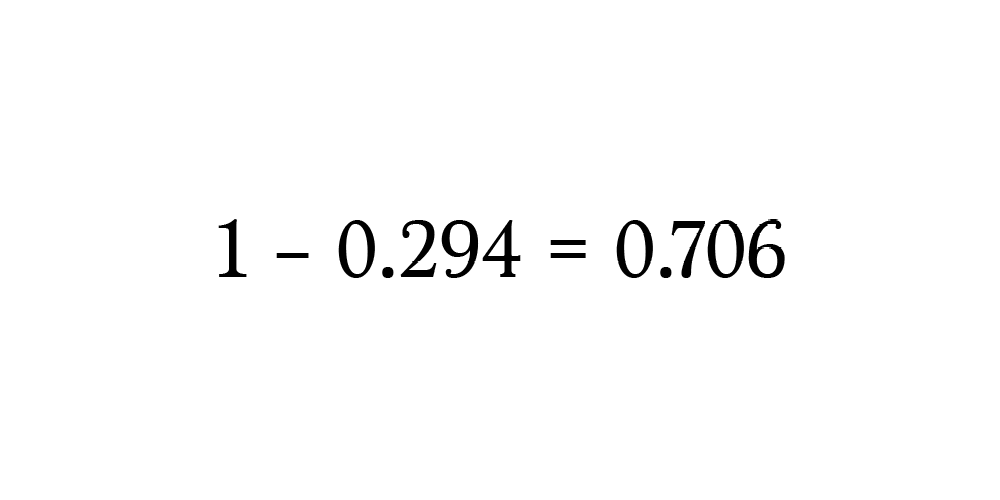
Получается, наш профессор сделал довольно безопасную ставку! У него был почти 71% вероятности того, что двое или более из нас родились в один день.

Шанс пятьдесят на пятьдесят

Знаете, чему многие удивляются? Если вы повторите этот расчёт с группой из 23 человек, то обнаружите 50% шанса, что во всяком случае двое человек родились в один и тот же день.

Это относительно маленькая группа людей с учётом 365 возможных дней рождения! И это означает, что в любом коллективе, где больше 23 человек, скорее всего, хотя бы 2 человека родились в один день. 

Какой безумный маленький факториал!

Что вас удивило больше: равенство 0,999 и 1 или проблема дня рождения?