🤤 Жадные алгоритмы: все, что нужно знать для собеседования

Жадные алгоритмы — это класс алгоритмов, которые на каждом шаге делают локально оптимальный выбор, полагая, что это приведет к глобально оптимальному решению в конце. Основные характеристики жадных алгоритмов:

• Локальная оптимальность — на каждом шаге алгоритм делает выбор, который кажется наилучшим, максимально выгодным в текущий момент (и может оказаться ошибочным в ретроспективе).
• Необратимость — выбор, сделанный на каждом шаге, не изменяется. Алгоритм не возвращается назад, чтобы изменить свое предыдущее решение.
• Постепенное построение решения — алгоритм строит решение шаг за шагом, добавляя к уже построенному частичному решению новые элементы.
  

Название «жадные» происходит от аналогии с человеком, который, стремясь к максимальной выгоде, хватает все самое ценное, что видит в данный момент, не задумываясь о долгосрочных последствиях. Жадный алгоритм точно так же всегда выбирает наилучший вариант из доступных, не учитывая влияние этого выбора на будущие шаги. В результате итоговое решение далеко не всегда оказывается оптимальным.

Примером оптимального решения с использованием жадного алгоритма может служить классическая задача о рюкзаке. Представьте, что вам нужно собрать рюкзак с максимальной ценностью вещей, но он имеет ограниченную вместимость (по объему или по весу). Жадный алгоритм в данном случае будет на каждом шаге выбирать самый ценный предмет, который помещается в рюкзак, пока он не заполнится. Алгоритм действует так:

• Рассчитывает стоимость единицы веса (или объема) для каждого предмета.
• Сортирует предметы по убыванию этой стоимости.
• Добавляет предметы в рюкзак, начиная с предмета с наибольшей стоимостью единицы веса/объема, пока позволяет оставшийся вес рюкзака.

Пример неоптимального решения — известная задача о выборе монет: здесь жадный алгоритм всегда будет проигрывать любому другому подходу, который способен просчитывать последствия своих действий на несколько шагов вперед.

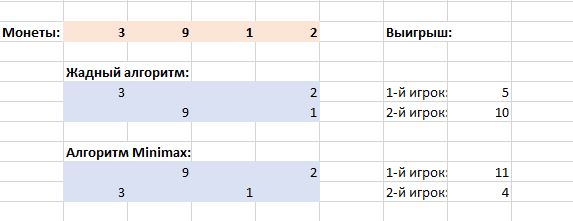
Предположим, имеется ряд монет [3, 9, 1, 2], выложенных в линию. Два игрока по очереди берут одну монету с любого конца ряда. Задача каждого игрока — максимизировать свою сумму. Игроки видят все монеты и знают, сколько стоит каждая монета.

Жадный алгоритм предполагает, что на каждом шаге игрок выбирает ту монету, которая имеет наибольшую стоимость из доступных с обоих концов. Это локально оптимальное решение, поскольку игрок выбирает максимально возможную монету в данный момент, не задумываясь о будущем:

• Первый игрок (И1) видит монеты 3 и 2 и выбирает 3 (так как она больше 2).
• Второй игрок (И2) видит монеты 9 и 2 и выбирает 9.
  
• Первый игрок (И1) видит монеты 1 и 2 и выбирает 2.
  
• Второй игрок (И2) берет оставшуюся монету 1.
  

Сумма для И1: 3 + 2 = 5

Сумма для И2: 9 + 1 = 10

В итоге И1 набрал 5, а И2 — 10. Жадный алгоритм проиграл, И1 не смог максимизировать свою сумму. Очевидно, для выигрыша нужно принимать во внимание будущие ходы и их последствия, и оценивать все возможные ходы противника, чтобы минимизировать его выгоду — как это делает, например, алгоритм минимакс.

Первый игрок (И1) размышляет:

• Если он возьмет 3, то второй игрок (И2) имеет выбор между 9 и 2.
• Если И2 выберет 9, то И1 останется с [1, 2].
  

И1 возьмет 2, И2 возьмет 1.

Сумма для И1: 3 + 2 = 5, сумма для И2: 9 + 1 = 10.

• Если И2 выберет 2, то И1 останется с [9, 1].

И1 возьмет 9, И2 возьмет 1.

Сумма для И1: 3 + 9 = 12, сумма для И2: 2 + 1 = 3.

• Если И1 возьмет 2, то второй игрок (И2) имеет выбор между 3 и 1.
• Если И2 выберет 3, то И1 останется с [9, 1].
  

И1 возьмет 9, И2 возьмет 1.

Сумма для И1: 2 + 9 = 11, сумма для И2: 3 + 1 = 4.

• Если И2 выберет 1, то И1 останется с [3, 9].

И1 возьмет 9, И2 возьмет 3.

Сумма для И1: 2 + 9 = 11, сумма для И2: 1 + 3 = 4.

Из анализа видно, что лучший ход для И1 — взять 2 в начале, что даст ему преимущество и лучшую итоговую сумму.

Курс «Алгоритмы и структуры данных» от Proglib Academy

Курс «Алгоритмы и структуры данных» предназначен для тех, кто хочет углубить свои знания в программировании, подготовиться к собеседованиям в ведущие IT-компании и участвовать в сложных проектах.

🎓 Почему стоит изучать алгоритмы

• Знание алгоритмов расширяет инструментарий разработчика.
• Подготовка к техническим собеседованиям в компании, такие как Яндекс, Сбер, Google, Microsoft и другие.
• Получение сертификата о прохождении курса от Proglib Academy

🔍 Что вас ждет

• 47 видеолекций и 150 практических заданий — программа, которая поможет вам освоить ключевые алгоритмы и структуры данных.
• Практическая направленность — написание кода и разбор алгоритмических задач.
• Поддержка преподавателей — комментарии по заданиям на протяжении всего курса.

💡 После курса вы сможете

• Создавать новые алгоритмы и структуры данных.
• Легко проходить технические собеседования.
• Применять полученные навыки в реальных проектах.

Преимущества и недостатки жадных алгоритмов

Жадные алгоритмы имеют свои достоинства, которые делают их оптимальными для решения задач определенного типа, и недостатки, о которых всегда нужно помнить.

Плюсы жадных алгоритмов:

• Простота и легкость в реализации — обычно просты для понимания и программирования, поскольку их логика основана на принятии максимально выгодных решений на каждом шаге.
• Скорость — как правило, имеют низкую вычислительную сложность, часто линейную или логарифмическую, что делает их подходящими для задач, требующих быстрого решения.
• Эффективность для определенных задач — отлично работают для ряда задач, где локально оптимальные решения приводят к глобально оптимальным. Например — задача о выборе мероприятий, обычная задача о рюкзаке и построение минимальных остовных деревьев.
• Небольшие требования к памяти — поскольку жадные алгоритмы делают решения на основе текущего состояния, они не требуют хранения большого количества промежуточных данных — это экономит память.
• Хорошее приближенное решение — даже если не гарантируют оптимального решения, часто дают хорошее приближение за разумное время.
  

Минусы жадных алгоритмов:

• Не всегда гарантируют оптимальное решение. Задачи, для которых нужно оценивать последствия действий (и иногда выбирать неоптимальные локальные опции для достижения глобального оптимума), не могут быть решены жадным алгоритмом эффективно.
• Ограниченная область применения и зависимость от структуры задачи. Жадные алгоритмы подходят только для тех задач, где локально оптимальные решения гарантированно ведут к глобально оптимальным. Например, жадный алгоритм подходит для решения задачи о размене монет, выпущенных в американской номинальной системе (1, 5, 10, 25, 50, 100/$1) и не подходит для такой же задачи, если в ней идет речь о размене монет из старой британской системы (1, 3, 6, 12, 24, 30). А если в задаче используются монеты, выпущенные в системе (1, r, r², r³), то лучшего решения, чем жадное, просто не найти.
• Отсутствие гибкости. Жадные алгоритмы следуют фиксированной стратегии выбора, не допуская изменений или улучшений решений по ходу выполнения. Они не адаптируются к изменениям условий или появлению новых данных. По этой причине с помощью жадного алгоритма нельзя решить задачу о рюкзаке 0-1.
• Потенциальная неоптимальность в реальных приложениях. Это следствие предыдущего пункта: в реальных задачах часто возникают ситуации, где жадные алгоритмы не могут учесть все нюансы и ограничения, и это приводит к неоптимальным или даже неверным решениям. Поэтому в реальных приложениях жадные алгоритмы используют в комбинации с другими подходами.

Главные особенности использования жадных алгоритмов

Жадные алгоритмы имеют свои плюсы и могут быть полезны в различных ситуациях, но их выбор и реализация требуют внимательного подхода:

• Жадные алгоритмы хорошо подходят для задач оптимизации, где нужно выбирать самые ценные опции из определенного набора вариантов. Например, в задаче о рюкзаке или задаче выбора мероприятий есть конкретные элементы, которые можно выбрать для достижения оптимального результата.
  
• Рекурсивное представление жадного алгоритма может быть проще для понимания и разработки, но для повышения производительности его следует реализовать итеративно.
  
• Жадный алгоритм не всегда приводит к оптимальному решению, но он может предоставить ценные идеи и помочь лучше понять структуру оптимального алгоритма. Также жадный алгоритм может служить в качестве эвристического метода, предоставляя быстрое и достаточно эффективное приближенное решение.
  
• В некоторых случаях выбор правильного жадного алгоритма может быть неочевидным, поскольку задачу можно решить несколькими жадными подходами. Поэтому всегда нужно проводить внимательный анализ задачи, чтобы понять, какое из жадных решений будет наилучшим.
  

Примеры задач, которые эффективно решаются с помощью жадных алгоритмов

Несмотря на некоторые ограничения и недостатки жадных алгоритмов, с их помощью можно оптимально решать задачи определенных типов. Рассмотрим несколько примеров.

Оптимальное распределение задач

Перед нами стоит проблема оптимального распределения задач между рабочими. Условия такие:

• Каждому рабочему должно быть назначено ровно две задачи.
• Каждая задача занимает фиксированное количество времени.
  
• Задачи независимы, то есть нет ограничений типа «задача 4 не может начаться до завершения задачи 3».
  
• Любая задача может быть назначена любому рабочему.
  

Требование к решению одно — распределить задания между исполнителями таким образом, чтобы минимизировать время завершения всех задач.

Решение:

Простое перечисление всех возможных пар задач нецелесообразно из-за слишком большого количества комбинаций:

Вместо этого следует обратить внимание на структуру задачи. Важно учесть минимальные и максимальные значения, поскольку имеет смысл сочетать задачи с большей продолжительностью с задачами с меньшей продолжительностью. Но это не означает, что решение сводится к сумме min и мах времени выполнения: если у нас есть задачи продолжительностью 1, 8, 9 и 10 часов, оптимальным временем выполнения всех работ будет не 1 + 10, а 8 + 9 часов. То есть вместо простого суммирования наибольшего и наименьшего значения нужно:

• Отсортировать продолжительности задач.
• Сочетать самую короткую задачу с самой длинной, вторую самую короткую — со второй самой длинной и т.д.
  
• Выбрать максимальный элемент из результирующего списка.
  

Предположим, есть 6 задач с продолжительностью 5, 2, 1, 6, 4 и 4 часа. Оптимальное распределение будет следующим:

• Первому рабочему — задачи с продолжительностью 1 и 6.
• Второму рабочему — задачи с продолжительностью 2 и 5.
  
• Третьему рабочему — задачи с продолжительностью 4 и 4.
  

При таком распределении все задачи будут завершены через max(1 + 6, 2 + 5, 4 + 4) = 8 часов:

        import collections

PairedTasks = collections.namedtuple('PairedTasks', ('task_1', 'task_2'))

def optimum_task_assignment(task_durations):
    task_durations.sort()
    return [
        PairedTasks(task_durations[i], task_durations[~i])
        for i in range(len(task_durations) // 2)
    ]

tasks = [5, 2, 1, 6, 4, 4]
assignment = optimum_task_assignment(tasks)
for i, pair in enumerate(assignment):
    print(f'Исполнитель {i + 1}: Задача 1 продолжительностью {pair.task_1} ч и Задача 2 продолжительностью  {pair.task_2} ч.')
print(f'Все работы будут выполнены за {max(assignment)[0] + max(assignment)[1]} ч.')
    

Вывод:

        Исполнитель 1: Задача 1 продолжительностью 1 ч и Задача 2 продолжительностью  6 ч.
Исполнитель 2: Задача 1 продолжительностью 2 ч и Задача 2 продолжительностью  5 ч.
Исполнитель 3: Задача 1 продолжительностью 4 ч и Задача 2 продолжительностью  4 ч.
Все работы будут выполнены за 8 ч.
    

Сложность этого решения — O(n log n), где n — количество задач, так как основное время выполнения алгоритма занимает сортировка.

Расписание для минимизации времени ожидания

В этой задаче требуется минимизировать общее время ожидания запросов к базе данных, учитывая заранее известное время обслуживания каждого запроса. Запросы должны быть обработаны по одному за раз и могут быть выполнены в любом порядке. Время ожидания запроса до его обработки называется временем ожидания этого запроса.

Сложность наивного решения с перебором всех возможных комбинаций огромна — O(n!), где n — число запросов. «Жадный» подход в этом случае намного эффективнее — он включает в себя:

• Сортировку запросов по времени обслуживания. Поскольку логично обрабатывать короткие запросы первыми, мы сортируем запросы по их времени обслуживания. Это позволяет нам упорядочить запросы таким образом, чтобы запросы с меньшим временем обслуживания были обработаны раньше.

• Обработку запросов в порядке возрастания времени обслуживания. После сортировки запросов мы обрабатываем их в порядке возрастания времени обслуживания. Это обеспечивает минимальное общее время ожидания, так как каждый запрос начинает обрабатываться сразу после завершения предыдущего запроса с меньшим или равным временем обслуживания.

Предположим, у нас есть следующие показатели времени обслуживания запросов: (2, 5, 1, 3). Если обработать запросы в порядке, указанном в списке, то общее время ожидания будет равно 0 + (2) + (2 + 5) + (2 + 5 + 1) = 17. При обработке запросов в порядке убывания времени обслуживания общее время ожидания увеличивается до 0 + (5) + (5 + 3) + (5 + 3 + 2) = 23. Но если расположить показатели по возрастанию для применения жадного алгоритма, можно получить самое оптимальное время обработки 0 + (1) + (1 + 2) + (1 + 2 + 3) = 10:

        def minimum_total_waiting_time(service_times):
    service_times.sort()
    
    total_waiting_time = 0
    for i, service_time in enumerate(service_times):
        num_remaining_queries = len(service_times) - (i + 1)
        total_waiting_time += service_time * num_remaining_queries
    
    return total_waiting_time

service_times = [2, 5, 1, 3]
print(minimum_total_waiting_time(service_times))
    

Вывод:

        10
    

Сложность этого решения определяется временем, затраченным на сортировку, и составляет O(n log n).

Задача покрытия интервалов

Эта задача заключается в том, чтобы помочь мастеру минимизировать количество посещений производственного цеха для проверки хода выполнения работ. Каждая задача начинается и заканчивается в определенное время. Мастер может посетить цех в любой момент времени и проверить все задачи, которые идут в этот момент. Необходимо найти минимальное количество посещений, которое позволит проверить все задачи.

Для решения подходит следующий жадный алгоритм:

• Сортировка интервалов. Сначала необходимо отсортировать все интервалы по времени окончания. Это позволит сосредоточиться на задачах, которые заканчиваются раньше.
• Выбор крайних точек. После сортировки интервалов выбирается время окончания первого интервала в отсортированном списке. Это время становится одним из моментов посещения мастера.
  
• Поиск следующего интервала. Далее алгоритм ищет первый интервал, который не покрыт уже выбранными моментами посещения. Как только такой интервал найден, его время окончания также выбирается в качестве момента посещения.
  
• Повторение процесса. Описанный выше этапы повторяются, пока не будут покрыты все интервалы.
  

Предположим, у нас есть следующие интервалы задач: [(1,2), (2,3), (3,4), (2,3), (4,5)]. После сортировки по времени окончания интервалов получаем: [(1,2), (2,3), (2,3), (3,4), (4,5)]. Первый выбранный момент посещения — это время окончания первого интервала, то есть 2. Этот момент покрывает первые три интервала. Далее ищем первый интервал, который не покрыт временем 2, и находим его — это (3,4). Выбираем время его окончания, 4, в качестве следующего момента посещения. Это покрывает оставшиеся интервалы.

Таким образом, минимальное количество посещений для проверки всех задач составляет 2 (в моменты 2 и 4):

        import collections
import operator

Interval = collections.namedtuple('Interval', ['left', 'right'])

def find_minimum_visits(intervals):
    intervals.sort(key=operator.attrgetter('right'))
    last_visit_time, num_visits = float('-inf'), 0
    for interval in intervals:
        if interval.left > last_visit_time:
            last_visit_time = interval.right
            num_visits += 1
    return num_visits


intervals = [
    Interval(1, 2),
    Interval(2, 3),
    Interval(3, 4),
    Interval(2, 3),
    Interval(4, 5)
]

print(find_minimum_visits(intervals)) 
    

Вывод:

        2
    

Другой способ решения:

        def min_points_cover_intervals(intervals):
    sorted_intervals = sorted(intervals, key=lambda x: x[1])
    points = []
    while sorted_intervals:
        point = sorted_intervals[0][1]
        points.append(point)
        sorted_intervals = [interval for interval in sorted_intervals if not(interval[0] <= point <= interval[1])]
    
    return points

intervals = [(1, 2), (2, 3), (3, 4), (2, 3), (4, 5)]
result = min_points_cover_intervals(intervals)
print(f"Минимальное количество посещений: {len(result)}, в моменты: {result}")  
    

Вывод:

        Минимальное количество посещений: 2, в моменты: [2, 4]
    

Временная сложность этого решения определяется сортировкой и равна O(n log n).

Подведем итоги

Жадные алгоритмы представляют собой мощный и эффективный метод решения определенных оптимизационных задач. Их главные преимущества — простота реализации и высокая скорость работы. Хотя жадные алгоритмы не универсальны и не всегда приводят к оптимальному решению, они служат отличной отправной точкой для разработки более сложных алгоритмов, а в некоторых случаях могут предоставить достаточно хорошее приближенное решение.

Статьи по теме

• 🅾️ Что такое «О» большое: объясняем на простых примерах
• 🙌 12 алгоритмов, которые должен знать каждый разработчик: объясняем на гифках
  
• 📐 10 алгоритмов для работы с графами, которые должен знать каждый кодер