Наталья Кайда 19 июня 2025

🤖 Математика для Data Science: терминология и обозначения

Для успешной работы с данными необходимы глубокие математические знания. Однако, прежде чем погрузиться в изучение продвинутых тем, важно освоить базовые математические обозначения и термины. Эта статья – первая часть путеводителя по основным символам, которые помогут вам уверенно читать и понимать книги и статьи по математической базе Data Science. Мы начнем с самых основ – действительных и комплексных чисел, затем перейдем к векторам и матрицам, после рассмотрим способы компактной записи сумм и произведений с помощью сигма- и пи-нотаций, а завершим обзором логарифмов.

Эта статья открывает серию публикаций, в которых мы подробно разберем все математические концепции, необходимые для успешной работы в Data Science. Основными темами станут:

Математические обозначения и терминология.
Случайные величины и распределения вероятностей.
Матрицы и линейная алгебра.
Функции потерь и оптимизация.
Вероятностное моделирование.
Временные ряды и прогнозирование.
Проверка гипотез.
Сложность модели.
Разложение функций.
Анализ сетей.
Динамические системы.
Ядерные методы.
Теория информации.
Непараметрические байесовские методы.
Случайные матрицы.

Все эти темы очень объемны, поэтому каждая из них будет рассмотрена в 2-3 статьях.

Математические обозначения

Математика – это язык, а математические символы и обозначения – его алфавит. Чтобы понимать книги и статьи по математической базе DS, важно хорошо разбираться в этом алфавите. Ниже мы рассмотрим основные математические обозначения и термины нескольких ключевых тем:

Действительные и комплексные числа.
Линейная алгебра (векторы и матрицы).
Суммы и произведения.
Логарифмы.

В следующей статье разберем обозначения и термины дифференциального и интегрального исчисления, математического анализа и комбинаторики.

Действительные и комплексные числа

В большинстве случаев дата-сайентисты работают с действительными числами (например, 4,6, 1 или -2,7). Их можно представить на числовой прямой:

Действительные (вещественные) числа – это все числа, которые можно представить на числовой прямой

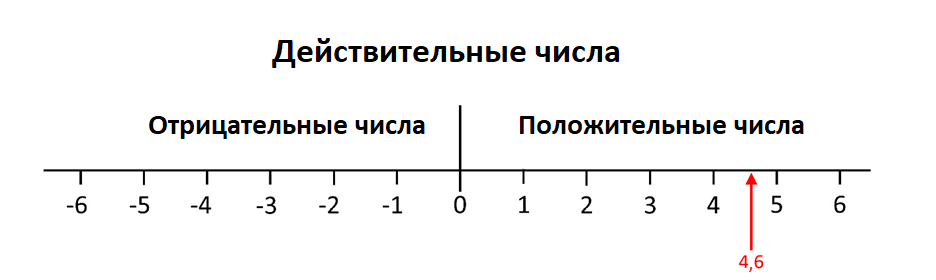
Множество всех действительных чисел обозначается символом ℝ.

Целые числа

В некоторых случаях данные могут быть ограничены только целыми числами. Целые числа (... , -2, -1, 0, 1, 2, ...) являются подмножеством действительных чисел и обозначаются символом ℤ. Как и действительных чисел, целых чисел бесконечно много.

Натуральные числа

Иногда данные ограничиваются только положительными целыми числами (например, в случае с движением товаров в онлайн-магазине). Это подмножество положительных целых чисел(1, 2, 3 и т. д.) называется натуральными числами. Натуральные числа обозначаются символом ℕ, в англоязычных источниках встречается также обозначение ℤ⁺.

Другие подмножества действительных чисел

В особых случаях возникает необходимость обратиться к другим подмножествам действительных чисел. Вы можете, например, встретить такие обозначения:

ℚ – множество рациональных чисел.
ℤ₂ – двухэлементное множество {0, 1}.

Последнее обозначение встречается при моделировании бинарных дискретных целевых переменных или при работе с бинарными признаками.

Курс математики для Data Science

Математика в Data Science — это не абстрактные формулы, а практический инструмент для понимания алгоритмов и решения бизнес-задач. Преподаватели ВМК МГУ вместе с Proglib Academy собрали программу, которая готовит к собеседованиям в топовые компании и поступлению в ШАД.

Комплексные числа

Если действительные числа «живут» на одномерной структуре, то есть на числовой прямой, возникает вопрос, можем ли мы использовать числа, «живущие» в двумерном пространстве. Да! Комплексные числа — это как раз такие числа. Множество комплексных чисел обозначается символом ℂ.

Комплексное число z имеет две составляющие: действительную часть x и мнимую часть y, где x и y – действительные числа. Действительная и мнимая части объединяются, и комплексное число z записывается в виде z = x + iy.

Символ i имеет особое значение. Это квадратный корень из -1, то есть i² = -1. Мы можем представить пару чисел (x, y) как точку на двумерной плоскости. Эта плоскость называется комплексной плоскостью или плоскостью Аргана:

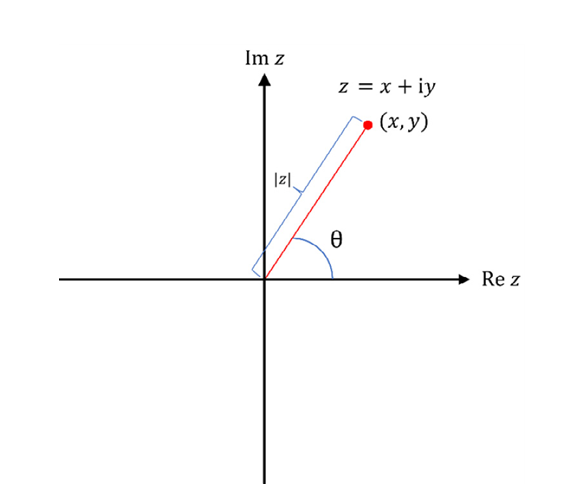
Плоскость Аргана используется для графического представления комплексных чисел

Положение комплексного числа z вдоль оси x (Re z) определяется его действительной частью, а положение вдоль оси y (Im z) — мнимой частью. Число, у которого мнимая часть y равна нулю, располагается полностью на оси x и является чисто действительным числом. Аналогично, комплексное число, у которого действительная часть x равна нулю, располагается полностью на оси y и является чисто мнимым числом.

Комплексные числа в полярных координатах

Как и в случае с другими двумерными плоскостями, точку на комплексной плоскости можно представить не только декартовыми координатами (x, y), но и полярными координатами, как показано на приведенной выше иллюстрации. Используя школьную тригонометрию, получим z = |z| × (cos θ + i sin θ). Символ |z| обозначает модуль комплексного числа z и совпадает с расстоянием от точки z до начала координат. Используя эту же иллюстрацию и теорему Пифагора, мы можем вычислить |z| следующим образом:

| z |^{2} = x^{2} + y^{2} = (Re z)^{2} + (Im z)^{2}

Угол θ обычно измеряется против часовой стрелки и в радианах, поэтому точка на положительной оси y будет иметь θ = π/2 (помните, что 2π радиан = 360°).

С учетом формулы Эйлера e^iθ = cos θ + i sin θ, которая связывает экспоненциальную и тригонометрическую формы комплексных чисел, мы также можем записать z в следующем виде:

z = | z | e^{i θ}

Эта последняя форма записи комплексного числа пригодится нам при изучении преобразования Фурье, которые используются для представления функций в виде суммы синусоидальных и косинусоидальных волн. Фактически, это и есть главная причина для изучения комплексных чисел в рамках курса по Data Science.

Комплексно-сопряженные числа

Важной концепцией, связанной с комплексным числом z, является его комплексно-сопряженное число. Комплексно-сопряженное число z мы обозначим как z̅. Иногда вместо этого используется символ z*. Комплексно-сопряженное число z̅ связано с z изменением знака мнимой части z: если z = x + iy, то z̅ = x – iy. На рисунке это показано простым отражением z относительно оси x. Полезное соотношение, которое из этого следует:

z \overset{―}{z} = x^{2} + y^{2} = | z |^{2}

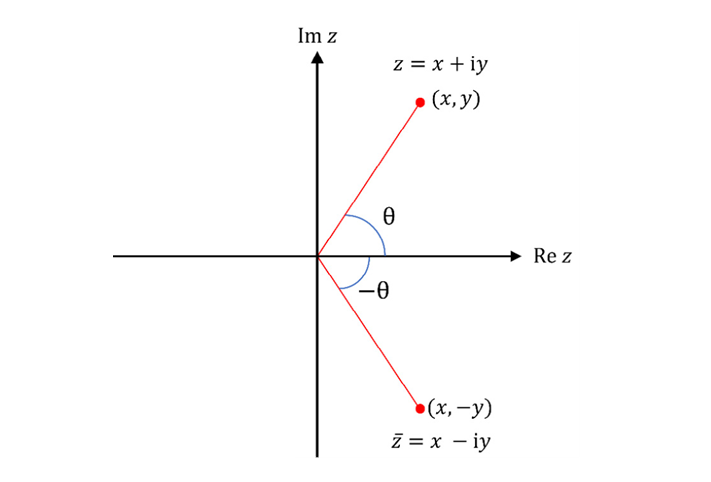
Комплексно-сопряженные числа получаются зеркальным отражением друг друга относительно действительной оси

Переменные и определение их типов

Все рассмотренные выше числа имеют конкретное значение, однако при описании алгоритмов или кода мы будем использовать переменные, обозначаемые символами типа x, которые могут принимать различные значения в зависимости от контекста.

При документировании алгоритма можно указать, что переменная x, к примеру, всегда будет действительным числом. Это обозначается как x ∈ ℝ, что на математическом языке означает «x принадлежит множеству действительных чисел» или, кратко, «x – действительное число».

Аналогично, если нужно указать, что x всегда является положительным целым числом, мы напишем x ∈ ℕ. Или, если x является комплексным числом, напишем x ∈ ℂ.

Статья по теме

🔢 Математика для Data Science: необходимый минимум

Линейная алгебра

Векторы

Во многих ситуациях нужно представлять набор чисел. Например, числа 7,3 и 1,2 могут быть значениями двух признаков, соответствующих одной точке данных в обучающем наборе. Обычно такие значения объединяют в скобках и записывают их как (7.3, 1.2) или [7.3, 1.2]. Поскольку эти способы записи похожи на обозначение координат в пространстве, такую совокупность чисел называют вектором.

Символически векторы иногда записывают жирным шрифтом (например, v). Чаще вместо жирного шрифта используется черточка сверху:

\overset{―}{v}

Или снизу (в англоязычных источниках):

\underset{―}{v}

Вектор может быть двухмерным, как в приведенном примере, или d-мерным, если он содержит d компонентов. Строковый d-мерный вектор выглядит так:

v = (v_{1}, v_{2}, \dots, v_{d})

А столбцовый вектор записывают так:

v = [\begin{matrix} v_{1} \\ v_{2} \\ ⋮ \\ v_{d} \end{matrix}]

Транспонирование вектора

Можно преобразовывать строковые векторы в столбцовые и наоборот с помощью операции транспонирования, которая обозначается верхним индексом 𝑇:

v^{T} = [\begin{matrix} v_{1} & v_{2} & \dots & v_{d} \end{matrix}]

И наоборот:

(v^{T})^{T} = v

Матрицы

Матрица — это двумерный массив чисел. Например, следующая таблица чисел является матрицей:

A = [\begin{matrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \end{matrix}]

Матрица обозначается заглавной буквой, иногда с двойным нижним подчеркиванием (в англоязычных источниках):

\underset{―}{\underset{―}{A}}

Поскольку матрица – это двумерная структура, ее размерность определяется двумя числами – m (число строк) и n (число столбцов). Чтобы обратиться к конкретному элементу матрицы, указывают номер его строки и столбца – Aij, т.е элементом А₂₃ в приведенной выше матрице является 7.

Типы матриц

Элементами матрицы могут быть любые числа. При этом:

Если все элементы – вещественные числа, то это вещественная матрица.
Если хотя бы один элемент комплексный, то это комплексная матрица.

Статья по теме

⚗️ 5 областей применения линейной алгебры в программировании

Суммы и произведения

Суммирование

Когда нам нужно сложить несколько чисел, мы используем суммирование (или сигма-нотацию), обозначаемую символом ∑ (греческая буква сигма).

Например, если мы хотим записать сумму чисел x₁ + x₂ + x₃ + x₄ + x₅, можно использовать сигма-нотацию:

\sum_{i = 1}^{5} x_{i}

Общее выражение суммы записывается так:

\sum_{i = m}^{n} x_{i}

где:

i – индексная переменная;
m – нижний предел суммирования;
n – верхний предел суммирования;
x_i – слагаемые, зависящие от i.

Эта запись означает: «Возьми все числа x_i, начиная с i = m и заканчивая i = n, и сложи их». Иногда в выражении ∑ опускают верхний и нижний пределы, если из контекста понятно, какие значения принимает индекс:

\sum x_{i}

Суммирование значений функций

Сигма-нотацию можно использовать не только для сложения самих элементов x_i, но и для сложения значений функции f(x_i). В общем виде формула выглядит так:

\sum_{i = m}^{n} f (x_{i})

Например, если у нас есть пять чисел x₁, x₂, x₃, x₄ и x₅, и мы хотим сложить их синусы, то запишем:

\sum_{i = 1}^{5} \sin (x_{i})

Суммы с индексной переменной

Сигма-нотацию можно применять и к выражениям, зависящим от индекса i, а не только от заранее заданных чисел. Например, сумма первых 100 квадратов (1²+ 2²+ 3²+ ⋯ + 100²) записывается так:

\sum_{i = 1}^{100} i^{2}

Произведение

Для компактной записи произведения нескольких чисел используется символ ∏ (заглавная буква пи):

Произведение чисел x₁, x₂, ..., x₅:

\prod_{i = 1}^{5} x_{i} = x_{1} \times x_{2} \times x_{3} \times x_{4} \times x_{5}

Произведение чисел x₁, x₂, ..., x_N:

\prod_{i = 1}^{N} x_{i} = x_{1} \times x_{2} \times . . . \times x_{N}

Произведение значений функции f(x_i):

\prod_{i = 1}^{N} f (x_{i}) = f (x_{1}) \times f (x_{2}) \times . . . \times f (x_{N})

Логарифмы

Логарифмы помогают понять, как быстро растет величина или функция, поскольку показывают, в какую степень нужно возвести основание, чтобы получить заданное число. Математически это записывается как log_a(a^x) = x. Например, log₂(8) = 3, так как 2³ = 8.

Чаще всего используются логарифмы с тремя основаниями:

10 (десятичный логарифм);
2 (двоичный логарифм);
e (натуральный логарифм, где e ≈ 2,718.

Из них натуральный логарифм с основанием e встречается настолько часто, что для него введено специальное обозначение ln, то есть ln x равнозначно log_ex.

В математике и в большинстве языков программирования, если используется просто log x без указания основания, то обычно подразумевается натуральный логарифм ln x. К примеру, функция numpy.log(y) в NumPy возвращает натуральный логарифм y. Однако в некоторых областях, например в инженерии, log x может означать десятичный логарифм log₁₀x, поэтому важно учитывать контекст.

Логарифмирование «уменьшает» число. Например, логарифм 1 000 000 по основанию 10 равен 6, потому что 10⁶ = 1 000 000. Это позволяет работать с очень большими числами. Более того, это также означает, что функция логарифма является монотонной, так что log(x) увеличивается с увеличением x:

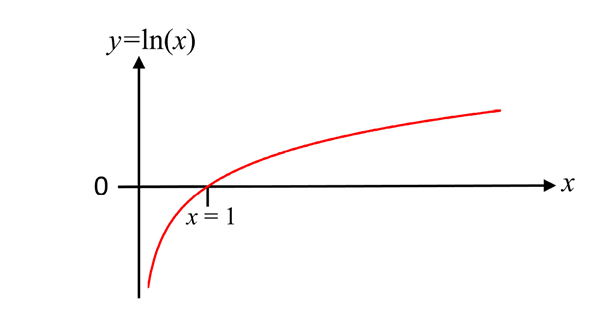
Чем больше число x, тем больше его логарифм

Важное следствие монотонного возрастания логарифмической функции заключается в том, что максимумы функции и ее логарифма достигаются в одной и той же точке. Математически этот факт можно записать так:

Если f (x) \leq f (x^{*}) при x \neq x^{*}, то \log f (x) \leq \log f (x^{*}) при x \neq x^{*}

Это свойство логарифма часто используется в математике и статистике для упрощения задач оптимизации — иногда проще найти максимум логарифма функции, чем максимум самой функции. Например, такой подход применяется в методе максимального правдоподобия для оценки параметров статистических моделей.

Основные действия с логарифмами

Эти правила справедливы для логарифмов с любым основанием:

Логарифм обратной величины равен отрицательному логарифму исходной величины:

\log_{a} (\frac{1}{y}) = - \log_{a} (y)

Логарифм произведения двух чисел равен сумме логарифмов этих чисел:

\log_{a} (x y) = \log_{a} (x) + \log_{a} (y)

Логарифм отношения двух чисел равен разности логарифмов этих чисел. Это правило выводится из предыдущих двух правил:

\log_{a} (\frac{x}{y}) = \log_{a} (x) + \log_{a} (\frac{1}{y}) = \log_{a} (x) - \log_{a} (y)

Логарифм произведения N чисел равен сумме логарифмов этих чисел. Этот факт пригодится в дальнейшем, когда мы начнем использовать понятие максимального правдоподобия для построения вероятностных моделей:

\log_{a} (\prod_{i = 1}^{N} x_{i}) = \log_{a} (x_{1} x_{2} \dots x_{N}) = \log_{a} (x_{1}) + \log_{a} (x_{2}) + \dots + \log_{a} (x_{N}) = \sum_{i = 1}^{N} \log_{a} (x_{i})

Подведем итоги

В этой статье мы рассмотрели четыре ключевых раздела математической нотации: теорию чисел, линейную алгебру, обозначения для сумм, произведений и логарифмов. В следующей статье мы продолжим наше путешествие в мир математического языка и разберем обозначения из области дифференциального и интегрального исчисления, математического анализа и комбинаторики – разделов, критически важных для понимания многих алгоритмов машинного обучения.

🤖 Библиотека Дата Сайентиста

Больше полезных материалов вы найдете на нашем телеграм-канале «Библиотека Дата Сайентиста»

🤖 Математика для Data Science: терминология и обозначения

Математические обозначения